|
Resumen
Realizaremos, desde cero y pautadamente, construcciones basadas en
vectores y construcciones cuyo
comportamiento vendrá dirigido por un corto guion de GeoGebra.
Concretamente, nos centraremos en analizar el gran potencial que surge al
asociar un guion a un deslizador con animación automática.
Información
Procedimientos pautados
 procedimientos
pautados.ggb
Este taller usa una plantilla ya preparada. Los objetos usados por
la propia plantilla son auxiliares, para ocultarlos de la Vista Algebraica.
Nota: Para
saltar de línea en un texto de la lista de instrucciones se usa \\n.
Parametrizaciones
En este documento (PDF,
DOC) se puede consultar información
técnica detallada para los profesores sobre las parametrizaciones que rigen
los objetos (rectas, cónicas, funciones, listas...) de GeoGebra.
Práctica
Recorridos y parametrizaciones
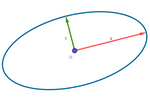
01 elipse vectorial.ggb
(resultado
final sin cuidar estética /
resultado final cuidando estética)
También resulta mucho más sencilla la manipulación de objetos geométricos
como las elipses si las definimos
vectorialmente sobre un sistema referencial relativo. De hecho, es lo que
hace el propio programa GeoGebra (ver PDF anterior sobre Animaciones automáticas).
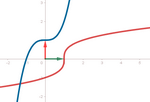 02
funciones
vectoriales.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Si redefinimos vectorialmente una función f(x) como O + t i + f(t)
j, donde {O, i, j} constituyen el sistema
referencial, basta intercambiar de posición los vectores i, j
para obtener la gráfica de la función inversa (cuyo dominio tal vez se
deba restringir, según los casos, para que sea efectivamente una función).
03 radián.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Si deseamos que la animación de dos
puntos en distintos recorridos corra a la misma velocidad “absoluta”,
deberemos calcular previamente la longitud de cada recorrido y dividir por
ella la velocidad del punto animado.
En el caso de que un recorrido tenga longitud infinita (como una recta o
una parábola), deberemos colocar el punto animado en una parte de longitud
finita (como
un segmento o un arco).
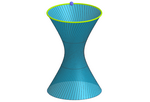
04 circuferencias e hiperboloide reglado
(resultado final sin cuidar estética /
resultado final cuidando estética)
En este ejemplo, gracias a las parametrizaciones, podemos conseguir la superficie
reglada simplemente retorciendo (es decir, desfasando) la circunfe-rencia
superior respecto a la inferior.
Modelizaciones
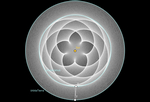
05 flor de Venus.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Los radios
medios de las órbitas de la Tierra y Venus alrededor del Sol apenas
influyen en la forma final. Lo que realmente define esta forma es la
fracción entre la duración de los ańos de Venus y la Tierra. El
denominador de la fracción indica cuántos ańos (terrestres) pasan hasta
repetir el ciclo.
06 órbitas elípticas.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Nota: Esta construcción fue realizada en colaboración con mi
compańero de departamento Julio Valbuena Herrero, quien adaptó la idea
expuesta por
Richard Feynman en su famoso lilbro The Feynman Lectures on Physics (1963,
volumen I
 ,
9-7, Planetary motions).
Trayectorias
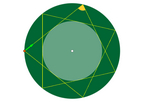
07 billar circular.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Si la banda es curva, en vez de recta, el eje de simetría es la
perpendicular a la recta tangente a la curva en ese punto. En el caso de un
billar circular, esa perpendicular es siempre el radio del círculo.
En el billar circular, todos los segmentos entre dos rebotes consecutivos
tienen la misma longitud. Dependiendo del ángulo de salida, podemos
determinar con facilidad el radio del círculo interior que quedará inscrito
en la trayectoria poligonal. También podemos encontrar cómo han de ser los
ángulos para que la trayectoria se cierre.
Además, en la construcción se usa un guion de GeoGebra para simular el
movimiento de la bola.
Atracciones y repulsiones
08 círculo con 5 puntos.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Crearemos un sistema dinámico que se estabilice por sí mismo:
Pongamos dos puntos en el interior de un círculo. Imaginemos que tanto los
puntos como el borde del círculo están cargados eléctricamente, con la misma
carga.
Los dos puntos se repelen entre sí, y son repelidos por la circunferencia,
con intensidad inversamente proporcional al cuadrado de la distancia. Inmediatamente, buscarán el equilibrio,
que se alcanzará cuando los dos puntos se dispongan simétricamente respecto
al centro del círculo y a una distancia entre sí igual a un tercio del diámetro.
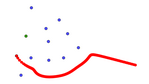 09
robot_entre_enemigos.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
Ahora crearemos un sistema dinámico jugando con la atracción y la
repulsión.
El robot (punto rojo P) conoce la
posición final que desea alcanzar (punto verde O) pero debe esquivar
una serie de enemigos (puntos azules).
Exploraciones dinámicas (robots)
 10
robot_recíproco_pitágoras.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
En este ejemplo, queremos demostrar de modo dinámico y automático el recíproco del teorema de Pitágoras.
Nota: Si queremos volver a repetir el experimento, debemos recordar
devolver inc al valor 0.1.
 11
robot_punto_fermat.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
En este otro ejemplo, queremos encontrar el punto de Fermat de un
triángulo dado. Para ello, hemos sustituido el papel del vértice C del
triángulo y de su alter ego C0 por un punto exterior al triángulo: F
y F0.
 12
robot laberinto.ggb
(resultado final sin cuidar estética /
resultado final cuidando estética)
En este último ejemplo, el robot ha de adaptarse al entorno: no tiene ninguna información sobre
la forma del laberinto. Solo detecta si hay espacio libre a su
derecha (en cuyo caso gira a la derecha para pegarse a la pared derecha)
o si hay un obstáculo enfrente (en cuyo caso gira a la izquierda).
|