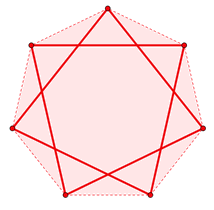
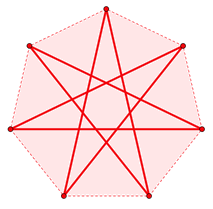
Cuando unimos los vértices de un polígono, saltando sistemáticamente un número dado de vértices, hasta volver al primero, la figura que nos resulta es un polígono estrellado. Así, por ejemplo, si partimos de un polígono de 7 vértices, un heptágono, según cómo unamos los vértices, podemos formar dos polígonos estrellados, como puedes ver más abajo. En el polígono de la izquierda el salto es 2 (contamos dos vértices a partir del primero y así sucesivamente, hasta cerrar el polígono), mientras que en el de la derecha el salto es 3 (contamos tres vértices a partir del primero y así sucesivamente).

Si el polígono del que partimos es un pentágono, solamente podemos formar un polígono estrellado (trata de razonar por qué no puede haber más que un polígono estrellado de 5 puntas). Se forma así una estrella que seguramente habrás visto muchas veces, pues es muy utilizada como símbolo o logotipo para diversos fines. Sabemos que ya era el símbolo de los seguidores del matemático griego Pitágoras y por eso suele llamarse estrella pitagórica. Observa algunos logotipos basados en la estrella de 5 puntas:

Vamos a trabajar ahora con polígonos estrellados de 5 puntas, como el que ves representado en la aplicación. Puedes mover sus vértices con lo que podrás formar estrellas muy diferentes. Al mover los vértices, los ángulos que forman los lados de la estrella también cambian, obviamente. Pero, ¿se mantendrá constante alguna relación entre esos ángulos? Eso es precisamente lo que vamos a investigar.

Preguntas

1. Haz clic sobre la casilla de "Mostrar transportador ". Utiliza el transportador para medir los ángulos de cada una de las puntas de la estrella. Puedes comprobar tus resultados haciendo clic en la casilla "Comprobar medida de ángulos". Con los datos que obtienes, completa la primera fila de la siguiente tabla. Suma los ángulos y escribe el resultado en la última casilla.

2. Mueve algunos vértices como creas conveniente. Ahora vuelve a medir los ángulos con el transportador y escribe en la tabla anterior los resultados, así como su suma, debajo de los que has escrito antes. Comprueba los resultados con la casilla de verificación. Desactiva la casilla después de la comprobación.

3. Mueve otra vez algunos vértices y repite el proceso de medición de ángulos y anotación de resultados.

4. Observa los resultados que vas obteniendo en la tabla, ¿observas alguna regularidad? Pon a prueba tu conjetura comprobando algún caso más (puedes ahorrarte la medida con el transportador y hacer los cálculos a partir de los datos que te proporciona la aplicación).

5. ¿Se cumplirá siempre esa relación? Vamos a tratar de demostrarlo. Pero antes es muy importante que recuerdes la relación que había entre ángulos en una circunferencia, concretamente entre el ángulo central (el que tiene el vértice en el centro) y el interior (tiene el vértice sobre la circunferencia) que abarcan el mismo arco. Para tratar de recordarlo vas a hacer algunas comprobaciones:

   1. Haz clic sobre el botón para volver a la situación inicial.

   2. Haz clic sobre la casilla "Mostrar ángulos centrales"

   3. Haz clic sobre la casilla "Mostrar transportador"

   4. Mide los dos ángulos rojos y compara los resultados.

   5. Haz lo mismo con los dos ángulos verdes y con los dos azules.

   6. ¿Recuerdas ahora la relación? Escríbela y ponla a prueba con los dos ángulos violetas.

6. ¿Cuánto suman los cinco ángulos centrales? Cuando mueves los vértices de la estrella, ¿cambia la suma de los ángulos centrales?

7. ¿Cuánto deben sumar los ángulos interiores, teniendo en cuenta la relación que has recordado en la pregunta 5? ¿Se corresponde ese resultado con el que has obtenido con tus mediciones?

8. Es el momento de escribir las conclusiones: ¿Cuánto suman los ángulos formados por las puntas de las estrellas en un polígono estrellado de 5 puntas? ¿Por qué?