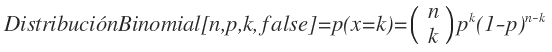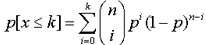Una de las tareas fundamentales en Estadística consiste en determinar, a partir de los resultados observados en una muestra, el modelo que sigue la distribución de una cierta variable en la población estudiada. Una vez determinado, para responder a las cuestiones que interesen bastará con aplicar las propiedades y características del modelo al que se ajusta.

Podemos sospechar que un conjunto de datos obtenidos experimentalmente se ajusta a una distribución binomial cuando se trata de N observaciones, relativas a n individuos de una población estadística, en cada una de las cuales se ha contado el número k de individuos que cumplen una determinada condición. De ese modo, para el análisis partimos de una tabla de frecuencias cuya variable toma los valores 0, 1, 2, ..., n.

Una distribución binomial queda caracterizada por los valores de n y p. En nuestro caso n ya es conocido, ya que viene determinado por los datos de partida. Sin embargo es necesario encontrar el valor de p.

Si la serie de datos experimentales se ajusta a una distribución binomial, la media, , de los datos ha de ser igual a la media de la distribución binomial B(n,p), , de modo que igualando ambas podemos obtener el valor de la probabilidad p:

El ajuste, y las ventajas que supone, carece de valor si no es suficientemente bueno. En todos los casos habrá diferencias entre los datos experimentales y los correspondientes según la ley ajustada, pero habrá que determinar en qué medida esas diferencias están justificadas por el azar, en cuyo caso la ley teórica ajustada es aceptable, o bien son demasiado grandes y debemos suponer que la ley teórica ajustada no es la que realmente siguen los datos experimentales y, por ello, se debe rechazar el ajuste. Para verificar si el ajuste es adecuado:

• Hallamos las probabilidades p[x=k] para k= 0, 1,2, 3, 4, ..., n, en la binomial B(n,p) y las multiplicamos por el número de observaciones realizadas para averiguar cómo se repartirían en la distribución teórica.

• Para cada valor de k, entre 0 y n, hallamos la diferencia entre el dato obtenido experimentalmente y el valor teórico.

• Valoramos las diferencias y, en función de ello, aceptamos o rechazamos el ajuste. En los problemas que vamos a abordar haremos una apreciación cualitativa de dichas diferencias. En próximos cursos veremos métodos más rigurosos para valorar la bondad de un ajuste.

Vamos a seguir los pasos citados para resolver el siguiente problema:

El control de calidad de cierto producto elige diariamente, al azar, un lote de 100 unidades y las inspecciona para ver si son correctas o han de rechazarse. En la siguiente tabla se reflejan los resultados de las 200 últimas inspecciones:

 

Nº de unidades rechazadas por lote	0	1	2	3	4	5	6	7	8	9	10	11	12
Nº de lotes	1	3	11	22	29	34	34	27	17	12	6	2	2

1. Calcula la ley teórica ajustada.
2. Si el producto se comercializa en cajas de 50 unidades, ¿cuál es la probabilidad de que en una caja no haya ninguna unidad incorrecta?
3. ¿Cuál es la probabilidad de que a lo sumo haya 5 unidades incorrectas en una caja de 50 unidades?
4. ¿Cuál es la probabilidad de que en una caja de 50 unidades haya más de 2 defectuosas?

Preguntas

1. En la tabla de frecuencias, observamos que el número de unidades rechazadas por lote varía entre 0 y 12. Sin embargo, teóricamente, ¿cuál es el número máximo de unidades que podría ser rechazado en un lote? ¿Cuál es el valor de n en la distribución binomial que buscamos para el ajuste?

2. Utilizando tu calculadora, calcula la media aritmética de los datos experimentales. ¿Qué significado tiene ese valor?

3. Conocidos n y , ¿cuánto debe valer la probabilidad p de la distribución binomial que buscamos? ¿Qué significa p en este caso concreto?

4. Vamos a hacer ahora los cálculos ayudándonos de la hoja de cálculo. Lo primero que haremos es añadir una columna a la tabla de frecuencias, a la derecha, con los productos de cada dato por su frecuencia. Para ello:

• Escribe en la barra de entrada la expresión: C2=A2 B2 (presta atención al espacio en blanco entre el 2 que sigue a la A y la letra B, de modo que GeoGebra interprete que es un producto). También podríamos haber escrito directamente en la celda C2 la expresión =A2 B2.

• Copia el contenido de la celda C2 en el rango C2:C14. Para ello haz clic sobre la celda C2 y sitúa el cursor en el cuadrado negro que aparece en su esquina inferior derecha. Manteniendo pulsado el botón izquierdo del ratón, mueve el cuadrado negro hasta seleccionar el rango C2:C14. Una vez seleccionado, suelta el botón izquierdo del ratón.

• Haz clic ahora sobre la celda C15. Elige la herramienta Suma y, a continuación, selecciona el rango C2:C14. De ese modo en la celda C15 tendremos el número total de lotes defectuosos en los datos experimentales.

• Utiliza el mismo procedimiento para escribir en la celda B15 la suma del rango B2:B14. Ese valor nos indica el número de observaciones que se han registrado.

• Escribe en la barra de entrada B16=C15/B15. De ese modo en la celda B16 obtendremos la media aritmética de los datos experimentales. Compárala con la que has obtenido en el apartado 1.

• En la celda B17 escribimos el valor de n. Escribe, en la barra de entrada, B17=100. También podríamos haber escrito el  número 100 directamente en la celda B17.

• Vamos a calcular ahora la probabilidad de la distribución binomial de ajuste. Escribe en la barra de entrada B18=B16/B17.

5. Con los datos que hemos obtenido, vamos a calcular ahora la distribución teórica de las 200 observaciones. Para ello:

• En la barra de entrada escribe: D2=$B$15 DistribuciónBinomial[$B$17,$B$18,A2,false]. Hemos utilizado el símbolo "$" para indicar que la referencia a la celda es absoluta, de modo que luego podamos copiar esa fórmula en el rango D2:D14 y en todos los casos los valores del número de observaciones, n y p se lean siempre en las celdas B15, B17 y B18, respectivamente. Hemos utilizado el comando Binomial[n,p,k,false], que nos proporciona la probabilidad p[x=k] en una binomial B(n,p):

• Copia ahora el contenido de la celda D2 en el rango D2:D14. Hemos obtenido de este modo el número de lotes teórico que corresponden a 0, 1, 2..., 12 unidades rechazadas.

• Sin embargo el número de lotes teórico debe ser un número entero, por lo que vamos a redondear los valores que acabamos de obtener. En la barra de entrada escribe: E2=round(D2). A continuación copia el contenido de la celda E2 en el rango E2:E14.

• Ahora, utilizando el procedimiento que ya conoces, halla en la celda E15 la suma del rango E2:E14. ¿Obtienes el resultado esperado? En caso de que la respuesta sea negativa, ¿a qué crees que es debido?

6. Ahora hemos de comparar la distribución teórica con los datos que habíamos obtenido experimentalmente. Para ello vamos a calcular las diferencias entre ambas distribuciones:

• Escribe, en la barra de entrada, la expresión: F2=E2-B2. A continuación, copia el contenido de la celda F2 en el rango F2:F14.

• Suma en la celda F15 los datos del rango F2:F14. ¿Obtienes el resultado esperado? En caso de que la respuesta sea negativa, ¿a qué crees que es debido?

7. Compara ahora los gráficos de ambas distribuciones. Activa la casilla Mostrar gráfico de la distribución y compara los gráficos.

8. Haz una valoración de los resultados que has obtenido en los apartados anteriores. ¿Está justificado el ajuste por la binomial B(n,p)?

9. Si el producto se comercializa en cajas de 50 unidades, ¿cuál será en ese caso la distribución teórica ajustada?

10. Vamos a utilizar la herramienta Cálculo de Probabilidades para los cálculos que se proponen. Selecciona la herramienta y observa que se abre una ventana emergente. En el tipo de distribución selecciona Binomial. Escribe, en las casillas correspondientes, los valores de n y p. Recuerda que ahora n=50. El valor de p lo has calculado en la celda B18, por lo que, para no perder precisión, escribe en la casilla directamente la referencia de la celda: B18.

11. Observa la tabla de valores que aparece en la parte superior derecha de la ventana emergente, una vez introducidos los valores de n y de p. ¿Qué información proporciona? ¿Podemos consultar en esta tabla cuál es la probabilidad de que no haya ninguna unidad defectuosa en una caja de 50 unidades?

12. Observa que para el cálculo de una probabilidad, en la parte inferior de la ventana emergente, antes hay que optar entre Intervalo (cuando se trata de hallar p[k1≤x≤k2], dados k1 y k2), Por Lado Izquierdo (cuando se trata de calcular p[x≤a], dado a] o Por Lado Derecho (cuando se trata de calcular p[x≥k], dado k). ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que no haya ninguna unidad defectuosa en una caja de 50 unidades? ¿Qué valor obtienes?

13. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que a lo sumo haya 5 unidades defectuosas en una caja de 50 unidades? ¿Qué valor obtienes?

14. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que haya más de 2 unidades defectuosas en una caja de 50 unidades? ¿Qué valor obtienes?

15. Cierra la ventana emergente que has abierto para los cálculos anteriores. Ahora vamos a efectuar los cálculos con la hoja de cálculo, utilizando el comando Binomial (Puedes ver aquí algunos ejemplos de su uso).

1. Calcularemos en la celda B19 la probabilidad de que no haya ninguna unidad defectuosa en una caja de 50 unidades. Para ello, escribe en la barra de entrada la expresión: B19=DistribuciónBinomial[50,B18,0,false].

2. Calcularemos ahora en la celda B20 la probabilidad de que a lo sumo haya 5 unidades defectuosas en una caja de 50 unidades. Para ello, escribe en la barra de entrada la expresión: B20=DistribuciónBinomial[50,B18,5,true]. Observa que el argumento empleado es ahora "true", con lo que el resultado del cálculo es, en este caso:

3. ¿Qué deberíamos escribir en la barra de entrada para calcular la probabilidad de que haya más de 2 unidades defectuosas en una caja de 50 unidades en la celda B21? Haz el cálculo correspondiente.