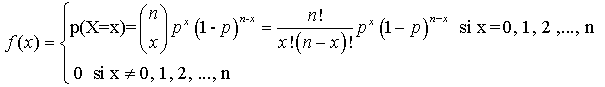Cualquier distribución de probabilidad que siga la ley binomial se caracteriza por:

• La experiencia aleatoria se compone de n experiencias simples cuyos resultados son independientes.

• En cada experiencia simple se observa exclusivamente si se presenta o no se presenta cierto suceso A.

• La probabilidad del suceso A es la misma en cada prueba p(A)=p. Evidentemente, también es constante en cada prueba la probabilidad del suceso contrario q=1-p.

• La variable aleatoria X considerada es el número de veces que ocurre A en las n pruebas, por lo que puede tomar los valores 0, 1, 2, ..., n. Su función de probabilidad es:

• Para identificar completamente la función de probabilidad de una distribución binomial basca con conocer el número de pruebas n y la probabilidad de éxito en cada prueba p: B(n,p).

Al tratarse de la repetición de n experiencias independientes, el número medio de veces que esperamos que ocurra el suceso A en las n pruebas realizadas será el producto de n por el número medio de veces que ocurra en una única prueba. Para la varianza, al tratarse también de una media (la media de los cuadrados de las diferencias con la media), sucederá lo mismo. Por lo tanto, los parámetros media o esperanza matemática, μ, y desviación típica, σ, de una distribución binomial B(n,p) son: