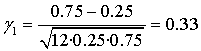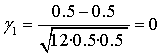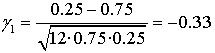|
La función de probabilidad de una distribución binomial se representa gráficamente mediante un diagrama de barras, en cuyo eje horizontal se disponen los valores de la variable aleatoria y la altura de cada una de las barras queda determinada por la probabilidad p[X=x].
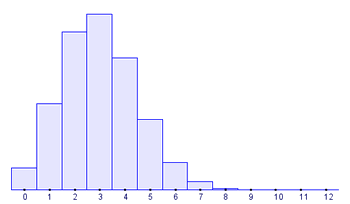
Así, la gráfica de la función de probabilidad de la distribución binomial B(12,0.25) es:
Gráfica 1: B(12,0.25)
Las características de la gráfica dependerán, por tanto, de los parámetros de la distribución binomial:
El valor de p también influye en la simetría de la gráfica, como podemos comprobar en las gráficas 1, 2 y 3, que se corresponden, respectivamente, con las funciones de probabilidad de las distribuciones binomiales B(12,0.25), B(12,0.5) y B(12,0.75):
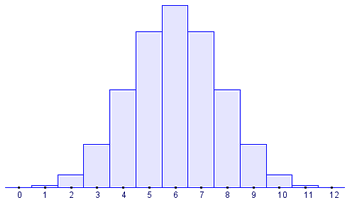
Gráfica 2: B(12,0.5)
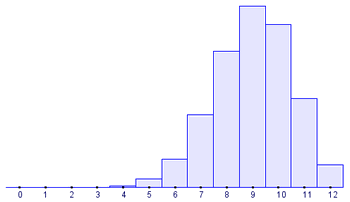
Gráfica 3: B(12,0.75)
La Gráfica 2, que es la que obtenemos cuando p=0.5, es simétrica. En la Gráfica 1, la "cola" a la derecha de la media es más larga que a la izquierda: diremos que hay una asimetría positiva o hacia la derecha. En cambio, en el Gráfico 3 la cola a la izquierda de la media es más larga que a la derecha: en ese caso hay asimetría negativa o hacia la izquierda. Para medir la asimetría se suele emplear el coeficiente de asimetría de Fisher:
En la Gráfica 1 tenemos una asimetría positiva o hacia la derecha:
En la Gráfica 2 el coeficiente de asimetría de Fisher es nulo:
En la Gráfica 3 la asimetría es negativa o hacia la izquierda:
|
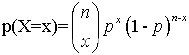
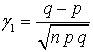 donde q = 1-p.
donde q = 1-p.