Para probar la eficacia de una vacuna, se administró a 150 grupos de 4 personas con riesgo de contagio y los resultados observados fueron los de la tabla siguiente:

Ajusta los datos a una distribución binomial, compara los resultados experimentales con los que se obtendrían con la distribución ajustada y valora la bondad del ajuste.

Utiliza la distribución binomial ajustada para calcular las siguientes probabilidades:

1. Si se administra la vacuna a un grupo de 5 personas, ¿cuál es la probabilidad de que se contagien dos personas?

2. Si se administra la vacuna a un grupo de 5 personas, ¿cuál es la probabilidad de que no haya ninguna persona contagiada?

3. Si se administra la vacuna a un grupo de 8 personas, ¿cuál es la probabilidad de que se contagien menos de 3 personas?

4. Si se administra la vacuna a un grupo de 8 personas, ¿qué probabilidad hay de que haya alguna persona contagiada?

5. Si se administra la vacuna a un grupo de 8 personas, ¿qué probabilidad hay de que se contagien entre 3 y 5 personas?

Preguntas

1. Utilizando tu calculadora, calcula la media aritmética 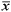de los datos experimentales. ¿Qué significado tiene el valor que has obtenido?

2. Conocidos n y 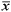, ¿cuánto debe valer la probabilidad p de la distribución binomial que buscamos? ¿Qué significado tiene p en este caso concreto?

3. Vamos a hacer ahora los cálculos ayudándonos de la hoja de cálculo. Lo primero que haremos es añadir una columna a la tabla de frecuencias, a la derecha, con los productos de cada dato por su frecuencia. Para ello:

• Escribe en la barra de entrada la expresión: C2=A2 B2 (presta atención al espacio en blanco entre el 2 que sigue a la A y la letra B, de modo que GeoGebra interprete que es un producto). También podríamos haber escrito directamente en la celda C2 la expresión =A2 B2.

• Copia el contenido de la celda C2 en el rango C2:C6. Para ello haz clic sobre la celda C2 y sitúa el cursor en el cuadrado negro que aparece en su esquina inferior derecha. Manteniendo pulsado el botón izquierdo del ratón, mueve el cuadrado negro hasta seleccionar el rango C2:C6. Una vez seleccionado, suelta el botón izquierdo del ratón.

• Haz clic ahora sobre la celda C7. Elige la herramienta Suma y, a continuación, selecciona el rango C2:C6. De ese modo en la celda C7 tendremos el número total de personas contagiadas.

• Utiliza el mismo procedimiento para escribir en la celda B7 la suma del rango B2:B6. Ese valor nos indica el número de grupos a los que se administró la vacuna.

• Escribe en la barra de entrada B8=C7/B7. De ese modo en la celda B8 obtendremos la media aritmética de los datos experimentales. Compárala con la que has obtenido en el apartado 1.

• En la celda B9 escribimos el valor de n. Escribe, en la barra de entrada, B9=4. También podríamos haber escrito el  número 4 directamente en la celda B9.

• Vamos a calcular ahora la probabilidad de la distribución binomial de ajuste. Escribe en la barra de entrada B10=B8/B9.

4. Con los datos que hemos obtenido, vamos a calcular ahora la distribución teórica de las 150 observaciones. Para ello:

• Escribe en la barra de entrada: D2=$B$7 DistribuciónBinomial[$B$9,$B$10,A2,false]. Hemos utilizado el símbolo "$" para indicar que la referencia a la celda es absoluta, de modo que luego podamos copiar esa fórmula en el rango D2:D6 y en todos los casos los valores del número de observaciones, n y p se lean siempre en las celdas B7, B9 y B10, respectivamente. Hemos utilizado el comando Binomial[n,p,k,false], que nos proporciona la probabilidad p[x=k] en una binomial B(n,p):

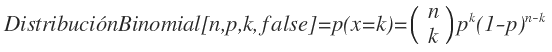
• Copia ahora el contenido de la celda D2 en el rango D2:D6. Hemos obtenido de este modo el número de grupos teórico en los que habría 0, 1, 2, 3 o 4 personas contagiadas.

• Sin embargo el número de lotes teórico debe ser un número entero, por lo que vamos a redondear los valores que acabamos de obtener. En la barra de entrada escribe: E2=round(D2). A continuación copia el contenido de la celda E2 en el rango E2:E6.

• Ahora, utilizando el procedimiento que ya conoces, halla en la celda E7 la suma del rango E2:E6.

5. Ahora hemos de comparar la distribución teórica con los datos que habíamos obtenido experimentalmente. Para ello vamos a calcular las diferencias entre ambas distribuciones:

• Escribe, en la barra de entrada, la expresión: F2=E2-B2. A continuación, copia el contenido de la celda F2 en el rango F2:F6.

• Suma en la celda F15 los datos del rango F2:F14. ¿Qué resultado obtienes? ¿Por qué?

6. Compara ahora los gráficos de ambas distribuciones. Activa la casilla Mostrar gráfico de la distribución y compara los gráficos.

7. Haz una valoración de los resultados que has obtenido en los apartados anteriores. ¿Está justificado el ajuste por la binomial B(n,p)?

8. Vamos a utilizar la herramienta Cálculo de Probabilidades para los cálculos que se proponen. Selecciona la herramienta y observa que se abre una ventana emergente. En el tipo de distribución selecciona Binomial. Escribe, en las casillas correspondientes, los valores de n y p. El valor de n es el número de personas del grupo al que se administra la vacuna. El valor de p lo has calculado en la celda B10, por lo que, para no perder precisión, escribe en la casilla directamente la referencia de la celda: B10.

9. Observa la tabla de valores que aparece en la parte superior derecha de la ventana emergente, una vez introducidos los valores de n y de p. ¿Qué información proporciona? ¿Cuál es la probabilidad de que se contagien exactamente dos personas si se administra la vacuna a un grupo de 5 personas?

10. Observa que para el cálculo de una probabilidad, en la parte inferior de la ventana emergente, antes hay que optar entre Intervalo (cuando se trata de hallar p[k1≤x≤k2], dados k1 y k2), Por Lado Izquierdo (cuando se trata de calcular p[x≤a], dado a] o Por Lado Derecho (cuando se trata de calcular p[x≥k], dado k). ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que se contagien exactamente dos personas si se administra la vacuna a un grupo de 5 personas? ¿Qué valor obtienes? ¿Coincide con el que has indicado en el apartado anterior?

11. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que no haya ninguna persona contagiada si se administra la vacuna a un grupo de 5 personas? ¿Qué valor obtienes?

12. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que se contagien menos de 3 personas si se administra la vacuna a un grupo de 8 personas? ¿Qué valor obtienes?

13. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que haya alguna persona contagiada si se administra la vacuna a un grupo de 8 personas? ¿Qué valor obtienes?

14. ¿Qué has de seleccionar y con qué límites para calcular la probabilidad de que se contagien entre 3 y 5 personas si se administra la vacuna a un grupo de 8 personas? ¿Qué valor obtienes?

15. Cierra la ventana emergente que has abierto para los cálculos anteriores. Ahora vamos a efectuar los cálculos con la hoja de cálculo, utilizando el comando DistribuciónBinomial (Puedes ver aquí algunos ejemplos de su uso).

    1. Calcula, en la celda B11, la probabilidad de que se contagien exactamente dos personas si se administra la vacuna a un grupo de 5 personas.

    2. Calcula, en la celda B12, la probabilidad de que no haya ninguna persona contagiada si se administra la vacuna a un grupo de 5 personas.

    3. Calcula, en la celda B13, la probabilidad de que se contagien menos de 3 personas si se administra la vacuna a un grupo de 8 personas.

    4. Calcula, en la celda B14, la probabilidad de que haya alguna persona contagiada si se administra la vacuna a un grupo de 8 personas.

    5. Calcula, en la celda B15, la probabilidad de que se contagien entre 3 y 5 personas si se administra la vacuna a un grupo de 8 personas.