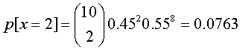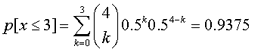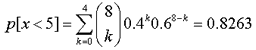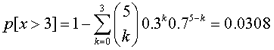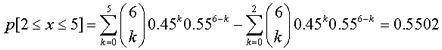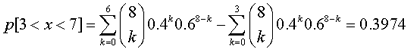|
Para calcular probabilidades en una distribución binomial
B(n,p) disponemos del comando DistribuciónBinomial[n,p,k,TF].
El parámetro TF es un valor booleano, que puede tomar los
valores "false" o "true", de modo que:
-
Binomial[n,p,k,false] = p[x=k]
-
Binomial[n,p,k,true] = p[x≤k]
Utilizando adecuadamente este comando podemos calcular
diferentes probabilidades, como podemos ver en los siguientes
ejemplos:
DistribuciónBinomial[10,0.45,2,false]
El resultado obtenido equivale a:
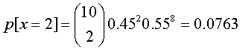
DistribuciónBinomial[4,0.5,3,true]
El resultado obtenido equivale a:
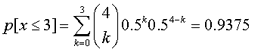
-
Para calcular la probabilidad p[x<5],
en una distribución binomial B(8, 0.4), tendremos en
cuenta que p[x<5]=p[x≤4],
por lo que escribiremos:
DistribuciónBinomial[8,0.4,4,true]
El resultado obtenido equivale a:
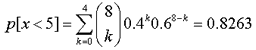
-
Para calcular la probabilidad p[x>3]
en una distribución binomial B(5, 0.3), tendremos en
cuenta que p[x>3]=1-p[x≤2],
por lo que escribiremos:
1-DistribuciónBinomial[5,0.3,2,true]
El resultado obtenido equivale a:
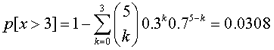
-
Para calcular la probabilidad p[3≤x≤5] en una distribución binomial
B(6, 0.45), tendremos en cuenta que esa probabilidad
equivale a p[x≤5]-p[x≤2],
de modo que escribiremos:
DistribuciónBinomial[6,0.45,5,true]-DistribuciónBinomial[6,0.45,2,true]
El resultado obtenido equivale a:
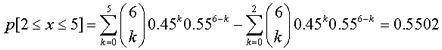
-
Para calcular la probabilidad
p[3<x<7], en una distribución binomial B(8, 0.4),
tendremos en cuenta que esa probabilidad equivale a p[x≤6]-p[x≤3],
de modo que escribiremos:
DistribuciónBinomial[8,0.4,6,true]-DistribuciónBinomial[8,0.4,3,true]
El resultado obtenido equivale a:
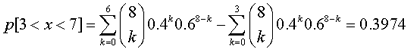
|