La derivada de una función en un punto mide el ritmo de crecimiento de la función en dicho punto. Ese ritmo de crecimiento, también conocido como tasa de variación instantánea, tiene una interpretación geométrica: es la pendiente de la recta tangente a la función en el punto considerado.

Por ello, si conocemos la recta tangente a la curva definida por una función, en un punto de la misma, podemos calcular la derivada de la función en dicho punto: será la pendiente de dicha recta, es decir, la tangente trigonométrica del ángulo que forma la recta tangente con el eje OX.

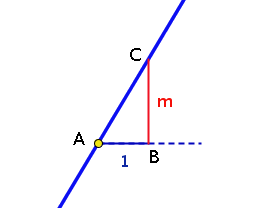
La pendiente de una recta, por otra parte, es fácil de calcular gráficamente. Basta observar la figura siguiente: si el cateto horizontal AB del triángulo ABC mide 1, la medida del cateto vertical BC de dicho triángulo es igual a la tangente del ángulo (tg A = m/1 = m) y, por tanto, a la pendiente de la recta.

Esta idea nos va a permitir obtener derivadas. En efecto, si a cada valor x₀ le hacemos corresponder el valor de la pendiente de la tangente a f(x) en dicho punto, es decir, en el punto (x₀, f(x₀)), estamos definiendo una nueva función, que llamaremos función derivada. La función derivada de una determinada función f(x) nos proporcionará la información necesaria para conocer la variación de f(x).

Con ayuda de la aplicación, vamos a descubrir la función derivada de algunas funciones conocidas.

Preguntas

1. Mueve el punto amarillo a izquierda y derecha y observa cómo varía la pendiente de la recta tangente. ¿Cuánto vale la derivada de la función en x=0? ¿Y en x=2? ¿Y en x=4? ¿Hay algún punto en el que la derivada sea 0? En caso afirmativo, indícalos.

2. Haz clic sobre la casilla "Mostrar rastro". Mueve el punto amarillo a izquierda y derecha y observa la función que se representa en color rosa. Describe qué ocurre cuando mueves el punto amarillo a izquierda y derecha. ¿Identificas la función representada? Halla su expresión algebraica. Utiliza la casilla "Comprobar la función derivada" para comprobar tu resultado.

3. Disponer de la función derivada es muy útil para el cálculo de la derivada en un punto. Utiliza la expresión algebraica de la función derivada para comprobar los valores que has calculado en el apartado 1.

4. Haz clic en para volver a los valores iniciales. En la casilla de entrada escribe f(x) = x^2 y pulsa la tecla INTRO (se trata de la función f(x)=x²). Activa la casilla "Mostrar rastro" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. ¿De qué función se trata? Escribe su expresión algebraica. Utilizando la expresión algebraica, halla la derivada de la función en x=-2, x=0 y x=2. Comprueba tus resultados con la aplicación.

5. Haz clic en . En la casilla de entrada escribe ahora f(x) = x^2 +2 y pulsa la tecla INTRO. Activa la casilla "Mostrar rastro" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. Cambia la función, escribe ahora f(x) = x^2 -3 y observa su función derivada. Haz lo mismo también con las funciones f(x) = x^2 +1 y f(x) = x^2 - 5. Compara los resultados que has obtenido en los casos anteriores, ¿qué conclusiones puedes sacar?

6. Haz clic en . Representa la función f(x)=sin(x). Para ello, en la casilla de entrada escribe: sin(x) y pulsa la tecla INTRO. Activa la casilla "Mostrar rastro" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. ¿De qué función se trata? Escribe su expresión algebraica. Comprueba tu resultado activando la casilla "Comprobar función derivada"

7. Utilizando la expresión algebraica, halla la derivada de la función en x=-2, x=0 y x=2. Comprueba tus resultados con la aplicación.

8. Haz clic en . En la casilla de entrada escribe: sin(x) + 2 y pulsa la tecla INTRO. Activa la casilla "Representar función derivada" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. Cambia la función, representa ahora f(x) = sin(x) - 3 y observa su función derivada. Haz lo mismo también con las funciones f(x) = sin(x)+1 y f(x) = sin(x) - 5. Compara los resultados que has obtenido en los casos anteriores, ¿qué conclusiones puedes sacar?

9. Haz clic en . Cambia ahora la función por f(x)=cos(x). Activa la casilla "Mostrar rastro" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. ¿De qué función se trata? Escribe su expresión algebraica. Comprueba tu resultado haciendo clic en la casilla "Comprobar función derivada".

10. Haz clic en . Cambia ahora la función por:  f(x) = exp(x) (se trata de la función f(x)=e^x). Activa la casilla "Representar función derivada" y mueve el punto amarillo a izquierda y derecha. Observa la función que se representa. ¿qué función se ha representado? ¿Cuál es la función derivada de f(x)=e^x?

11. Repite el proceso con las siguientes funciones: f(x) = x³ ; f(x) = ln(x). Completa la tabla con las funciones derivadas que has ido descubriendo hasta ahora.