|
Soluciones
-
Al variar la amplitud de los
armónicos, la cuerda adopta diferentes formas.
Primer armónico
-
Una vez fijado un valor t0
para el tiempo, la función será a1(x) = A1 sen(t0) sen(x),
cuya gráfica es una sinusoidal.
-
La cuerda aparecerá en su
posición horizontal de reposo cuando sen(t) = 0, es decir, para valores del
tiempo t múltiplos de 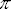 . .
-
El extremo derecho de la cuerda
tiene que corresponder al menor valor positivo para el cual sen(x) vuelva a
valer 0, es decir, al valor x =
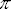 . .
-
No hay nodos.
-
La ecuación corresponderá al
valor del tiempo para el cual sen(t) sea máximo (es decir, 1). Por tanto la
función envolvente será E1(x) = A1 sen(x).
Segundo armónico
-
Corresponde al doble de
frecuencia que el sonido fundamental: 880 Hz.
-
La cuerda vibra el doble de
rápido que en el armónico anterior.
-
Una vez fijado un valor t0
para el tiempo, la función será a2(x) = A2 sen(2t0) sen(2x),
cuya gráfica es una sinusoidal.
-
La cuerda aparecerá en su
posición horizontal de reposo cuando sen(2t) = 0, es decir, para valores del
tiempo t múltiplos de 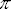 /2. /2.
-
Aparece un nodo en x =
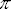 /2. /2.
-
La función envolvente será E2(x) = A2 |sen(2x)|.
Tercer armónico
-
Corresponde al triple de
frecuencia que el sonido fundamental: 1320 Hz.
-
La cuerda vibra el triple de
rápido que en el primer armónico, es decir, 3/2 más deprisa que en el armónico
anterior.
-
Una vez fijado un valor t0
para el tiempo, la función será a3(x) = A3 sen(3t0) sen(3x),
cuya gráfica es una sinusoidal.
-
La cuerda aparecerá en su
posición horizontal de reposo cuando sen(3t) = 0, es decir, para valores del
tiempo t múltiplos de 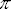 /3. /3.
-
Aparecen nodos en
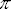 /3 y 2 /3 y 2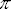 /3. /3.
-
La función envolvente será E3(x) = A3 |sen(3x)|.
Cuarto armónico
-
Corresponde al cuádruple de
frecuencia que el sonido fundamental: 1760 Hz.
-
La cuerda vibra el cuádruple de
rápido que en el primer armónico, es decir, 4/3 más deprisa que en el armónico
anterior.
-
Una vez fijado un valor t0
para el tiempo, la función será a4(x) = A4 sen(4t0) sen(4x),
cuya gráfica es una sinusoidal.
-
La cuerda aparecerá en su
posición horizontal de reposo cuando sen(4t) = 0, es decir, para valores del
tiempo t múltiplos de 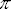 /4. /4.
-
Aparecen nodos en
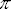 /4, /4,
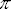 /2 y 3 /2 y 3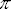 /4. /4.
-
La función envolvente será E4(x) = A4 |sen(4x)|.
Quinto armónico
-
Corresponde al quíntuple de
frecuencia que el sonido fundamental: 2200 Hz.
-
La cuerda vibra el quíntuple de
rápido que en el primer armónico, es decir, 5/4 más deprisa que en el armónico
anterior.
-
Una vez fijado un valor t0
para el tiempo, la función será a5(x) = A5 sen(5t0) sen(5x),
cuya gráfica es una sinusoidal.
-
La cuerda aparecerá en su
posición horizontal de reposo cuando sen(5t) = 0, es decir, para valores del
tiempo t múltiplos de 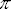 /5. /5.
-
Aparecen nodos en
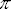 /5, 2 /5, 2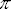 /5,
3 /5,
3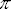 /5 y 4 /5 y 4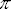 /5. /5.
-
La función envolvente será E5(x) = A5 |sen(5x)|.
Sumando armónicos
-
Para que la suma de todos los
armónicos genere una función de onda con forma de sierra, deben colocarse
todas las amplitudes al máximo. A partir de esta posición, para que aparezca
una forma de trapecios (onda cuadrada) deben anularse las amplitudes
pares y disminuir ligeramente el 3º armónico.
|