Resulta muy sencillo determinar la medida exacta de un segmento horizontal o vertical, cuyos extremos son puntos de un geoplano: solamente necesitamos contar los intervalos de separación entre los extremos. Sin embargo no resulta inmediato determinar su longitud exacta cuando se trata de un segmento trazado según alguna de las líneas oblicuas del geoplano. En esta actividad vamos a investigar cómo podemos calcular de manera indirecta la medida exacta de tales segmentos. También estableceremos algunas relaciones entre estos segmentos, que nos servirán para comprender un poco mejor la naturaleza de los números que manejaremos.

Utiliza las herramientas y para dibujar un segmento sobre el geoplano y para mostrar su medida exacta, respectivamente. En ambos casos, una vez seleccionada la herramienta, debes hacer clic en los dos extremos del segmento. Ten en cuenta que la unidad de medida es el centímetro, que es la separación entre dos puntos consecutivos en las líneas horizontales y verticales del geoplano o, dicho de otro modo, la longitud del lado del cuadrado mínimo que podemos construir sobre dicho geoplano.

Si te equivocas en algún momento, usa los botones de Deshacer y Rehacer o la herramienta Borrar .

Preguntas

1. Activa la casilla "Segmento 1". Activa también la casilla "Cuadrado sobre segmento". ¿Cuál es el área de este cuadrado? Puedes activar también la casilla "Cuadrado marco" para hacer más fácilmente tu cálculo.

2. Ya conoces el área del cuadrado construido sobre el segmento verde, ¿cómo puedes determinar ahora la longitud del segmento verde? ¿Cuál es su longitud exacta? ¿Puedes expresar esa longitud, de manera exacta, mediante un número decimal?

3. También podríamos utilizar el Teorema de Pitágoras para calcular la longitud del segmento. ¿Qué triángulo rectángulo podemos utilizar para el cálculo? ¿Qué representa el segmento verde en dicho triángulo? ¿Cuál es su longitud? Utiliza la herramienta para comprobar tu resultado. ¿Obtienes el mismo resultado que en el ejercicio anterior?

4. Haz clic en el botón Reiniciar. Activa ahora la casilla "Segmento 2". ¿Cuál es la longitud de este segmento? Utiliza los dos procedimientos de los ejercicios anteriores para determinarla (cuadrado construido sobre el lado y teorema de Pitágoras, respectivamente).

5. Construye un segmento que mida el doble que el segmento 2. Calcula su longitud exacta utilizando alguno de los procedimientos anteriores. Comprueba tu resultado con la herramienta .

6. Teniendo en cuenta que 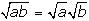, ¿puedes justificar aritméticamente la relación que existe entre el segmento 2 y el que tú has construido?

7. Haz clic en el botón Reiniciar. Activa ahora las casillas "Segmento 1" y "Segmento 3". ¿Qué relación hay entre las longitudes de estos dos segmentos? Ya conoces la longitud del segmento 1, por tanto, ¿cuál debe ser la longitud del segmento 3? Calcula ahora la medida exacta del segmento 3 utilizando el método del cuadrado sobre el lado y también mediante el teorema de Pitágoras. ¿Se confirma lo que habías supuesto?

8. Haz clic en el botón Reiniciar. Activa la casilla "Segmento 4". Calcula su medida exacta. ¿Puedes construir, uniendo puntos del geoplano, un segmento cuya longitud sea la mitad?

9. ¿Es cierta la relación 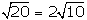? Trata de justificarlo aritméticamente.

10. Haz clic en el botón Reiniciar. Activa ahora las casillas "Segmento 5" y "Segmento 6" y halla su longitud exacta. ¿Se confirma lo que has contestado en el ejercicio anterior?

11. Haz clic en el botón Reiniciar. Activa ahora las casillas "Segmento 7" y "Segmento 8". ¿Qué relación existe entre sus longitudes?

12. Construye dos segmentos con los que puedas comprobar la relación: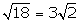

13. Haz clic en el botón Reiniciar. Activa la casilla "Segmento 3". Activa ahora la casilla "Cuadrado sobre segmento". Dibuja una diagonal del cuadrado que has dibujado. ¿Cuál es la medida exacta de esa diagonal?

14. Comprueba el teorema de Pitágoras en el triángulo rectángulo formado por dos lados contiguos del cuadrado y la diagonal correspondiente.

15. Haz clic en el botón Reiniciar. Construye un segmento que mida 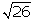cm.

16. Construye un cuadrado que tenga como diagonal el segmento de longitud 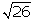cm del apartado anterior. ¿Cuánto mide el lado de ese cuadrado? Halla la respuesta a esta pregunta calculando la medida del lado utilizando alguno de los procedimientos que has utilizado en los primeros ejercicios y, a continuación, comprueba que obtienes el mismo valor aplicando el teorema de Pitágoras en el cuadrado que has construido.

17. Si el lado de un cuadrado tiene una longitud l, ¿cuál es la longitud de su diagonal?

18. Si la diagonal de un cuadrado tiene una longitud d, ¿cuál es la longitud de su lado?

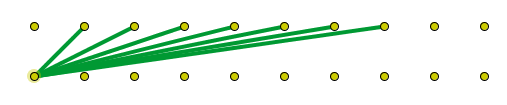
19. Imagina que unimos un punto del geoplano con todos los de la fila superior. En la imagen siguiente hemos representado algunos. ¿Qué relación existe entre sus longitudes? Si siguiéramos formando indefinidamente la secuencia (sin tener en cuenta la limitación de este geoplano), ¿encontraríamos entre ellos algún segmento de 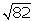cm de longitud? ¿Y de 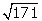cm?

20. Investiga los segmentos de diferente longitud que podemos construir en el geoplano (ten en cuenta que sus dimensiones son 9x14 cm), utilizando alguna diagonal, cuya longitud sea un número entero (ya has encontrado uno en el ejercicio 11).