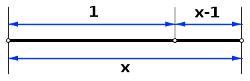
La primera referencia a la proporción áurea que se conoce la hace Euclides. En su obra los Elementos se refiere a la división de un segmento en lo que él denomina su media y su extrema razón del siguiente modo:

"Se dice que un segmento está dividido en media y extrema razón cuando el segmento total es a la parte mayor como la parte mayor es a la menor"

El valor de esta razón se conoce también como número de oro y suele representarse con la letra griega Φ (se lee Fi), en honor al escultor griego Fidias, que lo tuvo presente en sus obras.

Seguramente Euclides jamás pudo imaginar que esa división de un segmento, que definía únicamente para propósitos geométricos, llegaría a alcanzar tanta relevancia en la historia de la humanidad. Tal era la atracción que ejercía que Luca Pacioli, matemático italiano del siglo XV, la denominó divina proporción.

Podemos encontrarla en múltiples situaciones, que van de las artes a las ciencias, apareciendo como canon de belleza o ligada al crecimiento de especies vegetales o animales o, incluso, en la estructura de las galaxias. Esta proporción ha fascinado no solamente a muchos grandes matemáticos a lo largo de la historia, sino también a biólogos, artistas, músicos, historiadores, arquitectos, psicólogos e incluso místicos.

Preguntas

1. Mueve el punto amarillo que divide al segmento en dos partes. Observa las distancias de dicho punto a los extremos del segmento y compara la razón entre la longitud total del segmento y la de su parte mayor y la razón entre esta y la de su parte menor. ¿Puedes conseguir que ambas razones sean iguales? ¿Cuánto vale la razón, aproximadamente, en esa situación? Has encontrado un valor aproximado de la proporción áurea.

2. Vamos a calcular ahora el valor exacto de la proporción áurea. Supón que la longitud del segmento es x y que la parte mayor mide 1:

De ese modo x es el valor de la proporción áurea o número de oro que estamos buscando:

Resuelve la ecuación. ¿Cuántas soluciones obtienes? ¿Sirven todas? ¿Por qué? ¿Cuál es el valor exacto del número de oro?

3. ¿Podemos expresar en forma decimal el valor exacto del número de oro? ¿Por qué?

4. Haz clic sobre la casilla "Rectángulo 1". Desplaza el punto amarillo y observa cómo varía la forma del rectángulo. ¿Qué relación tienen sus dimensiones con la división que hacemos en el segmento?

5. Cuando los lados de un rectángulo están en proporción áurea recibe el nombre de rectángulo de oro. Mueve el punto amarillo hasta obtener un rectángulo de oro. ¿Cuáles son sus dimensiones?

6. Haz clic sobre la casilla "Rectángulo 2". Aunque los ves colocados en diferente posición, los dos rectángulos que aparecen son iguales. Fíjate en la recta roja trazada sobre la diagonal del rectángulo verde. Mueve el punto amarillo y observa la posición de la recta roja con respecto al rectángulo amarillo. ¿Qué ocurre cuando las dimensiones del rectángulo están en la proporción áurea? ¿Qué significado tiene?

7. El ejercicio anterior nos proporciona una forma muy sencilla de comprobar si las dimensiones de un rectángulo están en la proporción áurea o, al menos, se aproximan a ella. Muchos objetos que manejamos habitualmente tienen dimensiones que mantienen proporciones cercanas al número de oro, con lo que el método anterior nos va a permitir identificarlos. Vamos a ponerlo en práctica en varios casos.
   
   Haz clic en el botón Reiniciar. Activa la casilla Imágenes. Activa ahora la casilla "Tarjeta de crédito". Coloca las imágenes en la posición del ejercicio anterior. A continuación coloca la recta sobre la diagonal de la imagen horizontal, desplazando los puntos libres de la recta a los vértices de dicha diagonal. ¿Es un rectángulo áureo?

8. Activa la casilla "Rectángulo áureo". Utiliza ahora este rectángulo para comprobar si la tarjeta de crédito se aproxima a un rectángulo de oro. Para ello haz coincidir los vértices móviles del  rectángulo áureo con la imagen apaisada de la tarjeta de crédito y comprueba si coinciden ambos rectángulos.

9. Desactiva las casillas "Tarjeta de crédito" y "Rectángulo áureo" y activa la casilla DNI. Repite el procedimiento anterior y comprueba si el DNI electrónico es un rectángulo de oro.

10. Sigue el mismo procedimiento para comprobar si las dimensiones de la fotografía y del cuadro La última cena de Salvador Dalí están en la proporción áurea.

11. Desactiva la casilla Imágenes. Activa ahora la casilla "Rectángulo 1" y, a continuación, la casilla "Rectángulo 3". Demuestra que cuando el rectángulo ABCD es un rectángulo áureo, el rectángulo PBCE también lo es (observa que el rectángulo PBCE se obtiene al cortar el cuadrado APED al rectángulo ABCD).

12. El número Φ tiene algunas propiedades sorprendentes. Vamos a analizar algunas de ellas:

    1. Prueba que Φ² = Φ + 1

    2. Teniendo en cuenta la relación anterior, ¿encuentras alguna relación entre la parte decimal del número Φ² y la parte decimal de Φ?

    3. Prueba que el inverso de Φ tiene la misma parte decimal que Φ. (Pista: divide entre Φ los dos miembros de la igualdad que aparece en el apartado a)