-
Haz
clic sobre el botón  en la parte inferior de la
ventana para iniciar la animación y observa la posición de
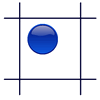
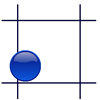
la ficha: si cae sobre alguna de las líneas de la
cuadrícula (el semáforo se pone en rojo) o no (el semáforo
se pone en verde). ¿Qué es más probable, que toque alguna
de las líneas de la cuadrícula o que no toque ninguna?
en la parte inferior de la
ventana para iniciar la animación y observa la posición de
la ficha: si cae sobre alguna de las líneas de la
cuadrícula (el semáforo se pone en rojo) o no (el semáforo
se pone en verde). ¿Qué es más probable, que toque alguna
de las líneas de la cuadrícula o que no toque ninguna?
Para apreciarlo mejor puedes parar la animación, con el
botón  ,
y mover despacio con el ratón la mano de la parte inferior
izquierda (actuando con el ratón sobre la ficha).
,
y mover despacio con el ratón la mano de la parte inferior
izquierda (actuando con el ratón sobre la ficha).
-
Cambia
el diámetro de la ficha, utilizando el deslizador azul.
Prueba con valores mayores y menores de 0.5. ¿De qué forma
dependen las posibilidades de que una ficha caiga sobre
una de las líneas de la cuadrícula de su diámetro?
-
Haz
clic sobre el botón  Reinicia y sitúa el deslizador
vertical en la posición Simulación. Con el botón
Reinicia y sitúa el deslizador
vertical en la posición Simulación. Con el botón  activa la
animación automática. Lo que observas son los resultados
de series de lanzamientos de 200 fichas iguales, de 0.5
unidades de diámetro, sobre una retícula cuadrada de lado
1 unidad. Fíjate en los resultados que aparecen en color
rojo en la parte superior, particularmente en la
proporción de fichas que tocan alguna de las líneas de la
cuadrícula.
activa la
animación automática. Lo que observas son los resultados
de series de lanzamientos de 200 fichas iguales, de 0.5
unidades de diámetro, sobre una retícula cuadrada de lado
1 unidad. Fíjate en los resultados que aparecen en color
rojo en la parte superior, particularmente en la
proporción de fichas que tocan alguna de las líneas de la
cuadrícula.
¿Qué proporción de fichas, por término medio, tocan alguna
de las líneas de la cuadrícula? Si lanzáramos 1000 fichas
iguales a las anteriores sobre la misma cuadrícula,
¿cuántas tocarían, por término medio, alguna de las líneas
de la cuadrícula?
-
Modifica
el número de fichas: prueba con otros valores. ¿Obtienes
resultados similares o hay variaciones importantes?
-
Con
los deslizadores selecciona 200 fichas de 0.25 unidades de
diámetro. Activa nuevamente la animación. ¿Qué proporción
de fichas, por término medio, tocan ahora alguna de las
líneas de la cuadrícula? Si lanzáramos 1000 fichas iguales
a las anteriores sobre la misma cuadrícula, ¿cuántas
tocarían, por término medio, alguna de las líneas de la
cuadrícula?
-
Con
los deslizadores selecciona ahora 200 fichas de 0.75
unidades de diámetro. Activa nuevamente la animación. ¿Qué
proporción de fichas, por término medio, tocan ahora
alguna de las líneas de la cuadrícula? Si lanzáramos 1000
fichas iguales a las anteriores sobre la misma cuadrícula,
¿cuántas tocarían, por término medio, alguna de las líneas
de la cuadrícula?
-
Analiza
los resultados de los cuatro ejercicios anteriores.
¿Encuentras alguna relación entre el diámetro de las
fichas y la proporción de fichas que toca alguna de las
líneas de la cuadrícula?
-
Haz
clic sobre el botón  Reinicia y sitúa el deslizador
vertical en la posición Solución. Ahora puedes mover
libremente la ficha sobre la cuadrícula, actuando con el
ratón sobre su centro. Activa la casilla "Mostrar rastro":
así podrás ver el rastro del centro de la ficha. Mueve la
ficha con cuidado por el interior del cuadrado, de modo
que no toque ninguna de las líneas de la cuadrícula.
Desliza la ficha sobre los lados del cuadrado, sin salirte
de los límites del mismo, y colorea también el interior
del recinto que delimitas.
Reinicia y sitúa el deslizador
vertical en la posición Solución. Ahora puedes mover
libremente la ficha sobre la cuadrícula, actuando con el
ratón sobre su centro. Activa la casilla "Mostrar rastro":
así podrás ver el rastro del centro de la ficha. Mueve la
ficha con cuidado por el interior del cuadrado, de modo
que no toque ninguna de las líneas de la cuadrícula.
Desliza la ficha sobre los lados del cuadrado, sin salirte
de los límites del mismo, y colorea también el interior
del recinto que delimitas.
Cuando lo hayas completado desactiva la casilla "Mostrar
rastro" y aparta la ficha para ver más claramente el
resultado. ¿Qué forma tiene la región que has coloreado?
¿Qué parte del cuadrado representa? Si consideramos que el
cuadrado tiene un área de 1 unidad cuadrada, ¿cuál es el
área de la región central coloreada? ¿Y el área de la
parte del cuadrado no coloreada? Si lo estimas necesario
haz clic sobre la casilla Ayuda.
-
Si
tras el lanzamiento el centro de la ficha cae en la región
no coloreada, la ficha tocará necesariamente alguna de las
líneas de la cuadrícula. Basándonos en esto podemos
calcular la probabilidad de este resultado, ya que será
igual a la proporción entre el área no coloreada y el área
total. Por tanto, ¿cuál es la probabilidad de que al
lanzar una ficha de 0.5 unidades de diámetro sobre una
cuadrícula de 1 unidad de lado toque alguna de las líneas
de la cuadrícula?
-
Utilizando
el mismo razonamiento calcula ahora las probabilidades de
que la ficha al caer toque alguna de las líneas de la
cuadrícula cuando su diámetro es de 0.25 unidades y cuando
sea de 0.75 unidades.
-
Compara
los resultados obtenidos en los dos últimos ejercicios con
los de la simulación anterior. ¿Qué conclusión puedes
sacar?