|
Vamos a ver cómo podemos
aprovechar la probabilidad para aproximar el resultado de cálculos complicados
sin necesidad de hacerlos. Como queremos comprobar que el método que vamos a
seguir funciona, buscaremos un resultado que ya conozcamos de antemano, por
ejemplo el valor del número
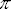 (aproximadamente 3.1416).
Pero no olvides que podríamos hacer lo mismo con valores que no conociéramos:
¡aquí está la fuerza de la probabilidad! (aproximadamente 3.1416).
Pero no olvides que podríamos hacer lo mismo con valores que no conociéramos:
¡aquí está la fuerza de la probabilidad!

Pulsa sobre esta imagen
para obtener más información
Prepararemos el
experimento. Observa la siguiente figura. Se trata de una diana circular de
radio 1 unidad inscrita en un cuadrado de lado 2 unidades. El área de la diana
es
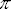 (unidades cuadradas), mientras que el área del cuadrado es de 4 unidades
cuadradas. (unidades cuadradas), mientras que el área del cuadrado es de 4 unidades
cuadradas.
|
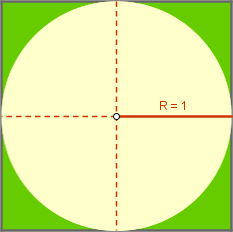 |
Área del círculo:
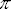 R2 = R2 =
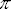 12 = 12 =
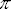
Área del cuadrado: 2 x 2 = 4 Por lo tanto, la fracción
de cuadrado ocupada por la diana es
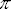 /4. /4. |
Ahora efectuamos muchos
disparos contra el cuadrado, completamente al azar. Todos darán en el cuadrado,
pero no todos darán en la diana. Contamos cuántos dan en cada uno. Si lanzamos
muchos, la fracción de disparos que darán en la diana (dianas/disparos)
deberá coincidir aproximadamente con la fracción de cuadrado ocupada por la
diana, que era la cuarta parte de
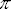 .
Así que bastará multiplicar por 4 la fracción dianas/disparos para obtener una
aproximación de .
Así que bastará multiplicar por 4 la fracción dianas/disparos para obtener una
aproximación de
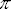 . .
Cuantos más disparos
realicemos, más probabilidad habrá de que nuestra aproximación de
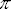 sea mejor. sea mejor.

Pulsa sobre esta imagen
para ver las instrucciones de uso
|