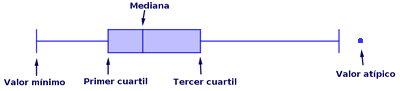
Para construir el diagrama de caja has de calcular previamente los valores necesarios para determinarlo: valor mínimo, primer cuartil, mediana, tercer cuartil y valor máximo.

La mediana está situada justamente en el medio de la distribución: el 50% de los datos es igual o inferior a la mediana y el otro 50% es igual o superior. Si en vez de partir la distribución en dos partes, por la mediana, la dividimos en cuatro, los valores que nos servirán de división se denominan cuartiles. El primer cuartil, que también suele llamarse cuartil inferior, deja por debajo al 25% de los datos y por encima al 75% restante. A su vez el tercer cuartil, o cuartil superior, deja por debajo al 75% de los datos y por encima al 25%. Lógicamente el segundo cuartil es la mediana. A la diferencia entre los valores de los cuartiles se la denomina recorrido intercuartílico y también es un parámetro importante. Análogamente podemos definir otras medidas de posición, como los deciles y los percentiles, que surgen cuando partimos la distribución en 10 o en 100 partes, respectivamente.

Un diagrama de caja, también llamado diagrama de caja y bigotes, está formado por un rectángulo, la caja, y dos segmentos, los bigotes, uno a cada lado del rectángulo. La caja abarca el recorrido intercuartílico, que es el intervalo comprendido entre el primer cuartil q₁ y el tercer cuartil q₃. Dentro de la caja se representa con un segmento la mediana de la distribución. El bigote izquierdo queda determinado por el valor mínimo y el primer cuartil y el derecho por el tercer cuartil y el valor máximo, excepto si existen valores atípicos.

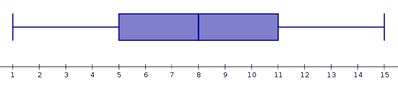
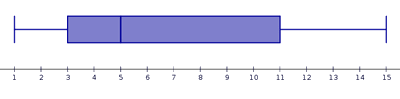
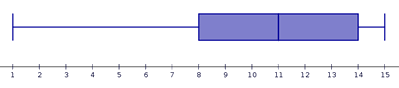
Se consideran valores atípicos los menores que q₁-1.5·(q₃-q₁) y los mayores que q₃+ 1.5·(q₃-q₁). Esto quiere decir que la longitud máxima de los bigotes es una vez y media la longitud de la caja (q₃-q₁). Cuando hay valores atípicos estos se representan fuera del diagrama de caja, mediante asteriscos o puntos.

Los diagramas de caja permiten una fácil lectura e interpretación del tipo de simetría de una distribución:

• Es simétrica cuando la media, mediana y moda de la distribución coinciden y los datos se distribuyen de igual forma a ambos lados de esas medidas.

• Es asimétrica positiva o sesgada a la derecha, cuando los datos tienden a concentrarse hacia la parte inferior de la distribución. La media se situaría a la derecha de la mediana.

• Es asimétrica negativa o sesgada hacia la izquierda cuando los datos tienden a concentrarse hacia la parte superior de la distribución. La media se situaría a la izquierda de la mediana.

Si una distribución es más o menos simétrica, la media aritmética y la desviación típica son parámetros muy adecuados para resumirla. Sin embargo cuando se trata de una distribución marcadamente asimétrica o sesgada resulta más adecuado utilizar el resumen de los cinco números: valor mínimo, primer cuartil, mediana, tercer cuartil y valor máximo.