De las tres medidas de centralización que solemos utilizar (media aritmética, mediana y moda), la media aritmética es la única que tiene en cuenta todos los datos de la distribución. Por eso se elige habitualmente cuando se trata de resumir en un único valor una colección de datos. Sin embargo tiene un inconveniente: su valor está muy influenciado cuando existen unas pocas puntuaciones extremas (valores atípicos). Aunque en menor medida, esos valores atípicos también tienen influencia sobre la desviación típica. Por ello, en tales casos, en vez de representar la distribución por su media y su desviación típica es preferible utilizar el resumen de los cinco números: valor mínimo, primer cuartil, mediana, tercer cuartil y valor máximo.

Muchas distribuciones estadísticas tienen un rasgo en común: algo más de las dos terceras partes de sus datos están contenidos en el intervalo comprendido entre la media menos la desviación típica y la media más la desviación típica. Esto nos permite estimar el valor de la desviación típica a partir de la gráfica de la distribución, evaluando la zona centrada en la media que recoja algo más de dos tercios de los datos o, de otro modo, la zona central que abarque algo más de dos tercios del "área" del histograma o diagrama de barras correspondiente.

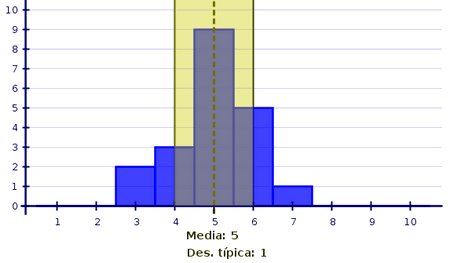
Observa el siguiente histograma, cuya área podemos considerar que es de 20 unidades (sumamos las frecuencias); el área de la parte del histograma comprendida dentro del intervalo [4,6] (media menos desviación típica, media más desviación típica) es de 13 unidades: