|
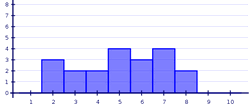
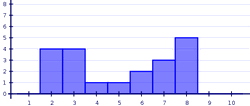
El histograma es uno de los gráficos estadísticos que manejamos más habitualmente. A partir del histograma podemos hacernos una idea bastante aproximada de la media aritmética y de la desviación típica de la distribución que se representa, que son, como sabes, dos de los parámetros que utilizamos para resumir un conjunto de datos.
Desde un punto de vista gráfico, la media aritmética coincide con el "punto de equilibrio" del histograma. En efecto, imagina por un momento que el gráfico es un objeto con masa y quisiéramos colocarlo en equilibrio sobre un punto de su eje horizontal: para conseguirlo el punto de apoyo ha de estar situado en la media aritmética, que es, por tanto, la proyección sobre el eje horizontal del centro de gravedad del gráfico.
Por su parte la desviación típica nos proporciona información sobre cómo están distribuidos los datos alrededor de la media: cuanto más alto sea el histograma en su zona central y más bajo en los laterales, menor será su desviación típica.
Además, en la mayoría de las distribuciones estadísticas algo más de las dos terceras partes de sus datos están contenidos en el intervalo comprendido entre la media menos la desviación típica y la media más la desviación típica. Esto nos permite estimar el valor de la desviación típica a partir de la gráfica de la distribución, evaluando la zona centrada en la media que recoja algo más de dos tercios de los datos o, de otro modo, la zona central que abarque algo más de dos tercios del "área" del histograma.
Basándote en lo anterior, en esta aplicación debes encontrar
los valores de la media aritmética y de la desviación típica de los histogramas
que se presentan. Después de completar el ejercicio y comprobar el resultado haz
clic en el botón |