En esta actividad partimos de la forma canónica de la ecuación de la función cuadrática y = a (x-x₀)² + y₀,  donde el coeficiente "a", en valor absoluto, es el inverso de la longitud del lado recto y su signo indica la orientación de la parábola de vértice V (x₀, y₀).

Usaremos la forma canónica para realizar el cálculo de las raíces de la función y los puntos de corte de la parábola con los ejes de coordenadas.

Preguntas

1. El cálculo del punto de corte de la parábola con el eje OY (eje de ordenadas) es muy sencillo, ya que en ese eje la abscisa siempre vale 0. Así que para averiguar el valor de la ordenada basta sustituir 0 como valor de la abscisa en la ecuación. Por ejemplo, el punto de corte de la parábola y =  (x-1)² -4 con el eje de ordenadas es (0, -3). Compruébalo con la aplicación colocando el vértice de la parábola en el punto V = (1, -4).
   
   ¿Cuál es el punto de corte con el eje de ordenadas de la parábola y = 3 (x-2)² -9?

2. Vamos a hallar los puntos de corte con el eje OX (eje de abscisas) de la parábola y = (x-4)² -4. Como en ese eje la ordenada siempre vale 0, hay que resolver la ecuación de segundo grado 0 = (x-4)² -4. Esta ecuación es fácil de resolver:
   
   
   
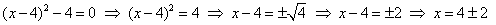
   Por lo tanto, las raíces son x₁ = 2, x₂= 6, y los puntos de corte de la parábola con el eje OX son (2, 0) y (6, 0). Compruébalo con la aplicación colocando el vértice de la parábola en el punto V = (4, -4).
   
   Emplea el mismo método para hallar las raíces de la función y = 2(x-3)² -8. Una vez halladas, comprueba que lo son sustituyendo su valor en lugar de "x" en esta ecuación para ver si efectivamente "y" toma el valor cero.

3. Encuentra los tres puntos de corte con los ejes de la parábola y = (x-2)² -1 y compruébalos con la aplicación.

Nota: Mientras que el punto de corte con el eje OY siempre existe (porque siempre existe un valor de y para x=0), no siempre hay puntos de corte con el eje OX. Eso dependerá de la orientación de la parábola y la situación del vértice.

Si la parábola está orientada hacia arriba (a>0), el vértice debe tener ordenada negativa para que la parábola corte el eje OX en dos puntos distintos (compruébalo con la aplicación).

De forma simétrica, si la parábola está orientada hacia abajo (a<0), el vértice debe tener ordenada positiva para que la parábola corte el eje OX en dos puntos distintos.

En el caso de que el propio vértice de la parábola tenga ordenada cero, ese será el único punto de corte con el eje OX  (compruébalo con la aplicación).

Como consecuencia, no todas las funciones cuadráticas tienen raíces reales, solo aquellas cuya gráfica parabólica corte el eje OX.