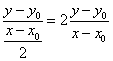En esta actividad partimos de la forma canónica de la ecuación de la función cuadrática y = a (x-x₀)² + y₀,  donde el coeficiente "a", en valor absoluto, es el inverso de la longitud del lado recto y su signo indica la orientación de la parábola de vértice V (x₀, y₀).

Vamos a resolver el problema concreto de encontrar la ecuación de la recta tangente a la gráfica de la función cuadrática y = (x-2)² + 1 en un par de puntos distintos de la parábola.

Preguntas

1. No cambies la posición de los puntos. Fíjate en el triángulo rectángulo azul, bajo la recta tangente. ¿Cuánto mide el cateto vertical NP? Recuerda que en la expresión "y - y₀", "y" es la ordenada del punto P e "y₀" es la ordenada del vértice V. Anota el número obtenido, correspondiente a esa resta, en tu cuaderno.

2. Recuerda que M era el punto medio entre V y N. ¿Cuánto mide el cateto horizontal MN del triángulo azul?

3. A partir de las respuestas anteriores, escribe el valor de la pendiente de la recta tangente a la parábola en el punto P (3, 2). Llamaremos a esa pendiente "m".

4. La ecuación de la recta tangente que pasa por el punto P (3, 2) será por tanto de la forma y = m x + n. Ya conocemos el valor de m, falta averiguar el valor de n. El punto P (3, 2), además de estar en la parábola, también pertenece a la recta tangente, así que tiene que cumplir su ecuación: 2 = m 3 + n. ¿Cuál es entonces el valor de n?

5. Escribe finalmente la ecuación de la recta tangente a esa parábola en el punto P (3, 2).

6. Mueve P hasta la posición (2.8, 1.64) y, siguiendo el mismo procedimiento, encuentra la ecuación de la recta tangente a esa parábola en el punto P.

Nota: Observa en el triángulo azul que la pendiente m de la recta tangente siempre será el cociente

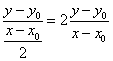
Como, a partir de la forma canónica tenemos que y - y₀= a (x-x₀)², sustituyendo y simplificando llegamos a que la pendiente de la recta tangente a una parábola siempre será de la forma m = 2a (x-x₀).