-
La distancia del foco a la
directriz, es decir, la longitud del segmento p, se conoce como
parámetro focal de la hipérbola. Recuerda que la hemos llamado "p" cuando
contestes a las siguientes preguntas. ¿Cuál es la proporción entre el cateto mayor y el menor del triángulo rectángulo verde?
-
Activa la casilla Proporción
constante. Explica qué se muestra y por qué. ¿Qué nombre recibe esa
proporción constante?
-
Desactiva la casilla "Proporción
constante". Activa la casilla Lado recto. En función del parámetro
focal y la excentricidad, ¿cuánto mide el lado recto de una hipérbola?
-
Desactiva la casilla "Lado
recto". Activa la casilla Eje principal, también llamado "eje
focal". Explica qué se muestra y por
qué.
-
Activa la casilla Primer
vértice. Siempre en función de p y e, ¿cuánto mide el radio
de la circunferencia que aparece? ¿Cuánto vale la distancia FR? El vértice V es un punto de la hipérbola, que
se encuentra en su eje principal. Como está en la hipérbola debe cumplir
que VF = e VD. ¿Por qué al trazar una paralela a DR por el punto E obtenemos
su posición exacta? (Pista: fíjate en los triángulos VFE y DFR.)
-
Desactiva la casilla "Primer
vértice". Activa la casilla Segundo vértice. ¿Cuánto vale la distancia FS? El vértice V' es un punto de la hipérbola, que se encuentra en
su eje principal. Como está en la hipérbola debe cumplir que V'F = e V'D.
¿Por qué al trazar una paralela a DS por el punto E obtenemos su posición
exacta?
-
Desactiva la casilla "Segundo
vértice". Activa la casilla Centro. El centro C es el punto medio
entre los vértices. Observa que también podemos obtenerlo trazando una
paralela a VS por el punto E. Eso significa
que FC = e VC, es decir, la proporción entre la distancia del foco
F al centro y
la distancia del vértice V al centro es también igual a la excentricidad. ¿Por
qué?
-
Desactiva la casilla Centro.
Activa la casilla Eje secundario. ¿Cómo se construye el eje secundario?
¿Cómo es la hipérbola respecto a ese eje?
-
Activa la casillas Segunda
directriz y Segundo foco. Explica qué se muestra y por qué. ¿Qué
relación existe entre los puntos de la hipérbola y estos nuevos elementos?
-
La hipérbola también se puede
definir como el lugar geométrico de los puntos del plano cuya diferencia (en
valor absoluto) de distancias a los dos focos es siempre constante. Esa
diferencia constante tiene que equivaler a la distancia entre los
vértices. ¿Por qué?
Nota: No es difícil deducir
que la diferencia (en valor absoluto) de distancias de cualquier punto de la
hipérbola a los focos ha de ser constante. Como un punto de la hipérbola dista
de cada foco la misma proporción (e) que de cada directriz, su diferencia de
distancias a los focos es proporcional a la diferencia de distancias a las
directrices, pero esta diferencia es (en valor absoluto) la distancia entre
las directrices, que es constante.
-
Activa la casilla Distancia
focal. ¿Cuál es la relación entre esta distancia entre los focos y la
distancia entre los vértices?
-
Desactiva la casilla "Distancia
focal". Activa la casilla Asíntotas. Son rectas a las que se aproximan
(sin llegar nunca a alcanzarlas) los brazos curvos de la hipérbola. ¿Qué
relación existe entre focos, vértices y las dimensiones del rectángulo azul?
¿Qué proporción guardan la diagonal y el ancho del rectángulo azul? ¿Cómo se
construyen las asíntotas?
-
¿Qué forma debe tener el
rectángulo para que las asíntotas sean perpendiculares? En ese caso particular
en que las asíntotas son perpendiculares, la hipérbola se denomina
hipérbola equilátera. ¿A qué crees que se debe este nombre? El valor de la
excentricidad de cualquier hipérbola equilátera será siempre el mismo,
exactamente
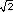 . ¿Por qué?
. ¿Por qué?