|
Preguntas
-
Mueve el vértice V. Puedes
colocarlo en el primer o en el segundo cuadrante. ¿Qué relación existe entre
las coordenadas de V y la ecuación de la función?
-
Haz clic en el botón
 Reiniciar.
Mueve ahora el centro C, aproximadamente 0.4 unidades hacia la derecha y hacia arriba (para favorecer la distinción de las dos hipérbolas que
aparecen). El movimiento que acabas de realizar se llama traslación. Al
trasladar el centro has trasladado también todos los puntos del plano: el
vértice V (muévelo), el punto P (muévelo) y toda la hipérbola se han desplazado por
igual, así que no han variado su posición relativa respecto a unos nuevos ejes
de coordenadas centrados en el nuevo centro C (x0, y0)
de la hipérbola. Reiniciar.
Mueve ahora el centro C, aproximadamente 0.4 unidades hacia la derecha y hacia arriba (para favorecer la distinción de las dos hipérbolas que
aparecen). El movimiento que acabas de realizar se llama traslación. Al
trasladar el centro has trasladado también todos los puntos del plano: el
vértice V (muévelo), el punto P (muévelo) y toda la hipérbola se han desplazado por
igual, así que no han variado su posición relativa respecto a unos nuevos ejes
de coordenadas centrados en el nuevo centro C (x0, y0)
de la hipérbola.
Considerando las coordenadas (x0, y0) del centro C, ¿qué
relación existe ahora entre la ecuación de la función y las coordenadas de V?
-
La posición de todos los puntos
de la hipérbola ha variado respecto a los ejes de coordenadas reales. Así que
para mantener la relación y = A/x que existía en todos los puntos de la
hipérbola
habrá que devolverlos a su anterior origen sumando a sus coordenadas el vector
de traslación opuesto: (-x0, -y0). Observa en la
construcción que, efectivamente, la posición del punto P respecto a los nuevos
ejes es (x-x0, y-y0). La nueva ecuación de la hipérbola
es, entonces: y-y0 = A/(x-x0), es decir, y = A/(x-x0) + y0.
Como y0 puede escribirse como y0(x-x0)/(x-x0),
comprueba que la ecuación anterior es equivalente a:
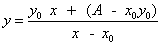
-
Esta ecuación puede
escribirse de la forma general y = (a x + b) /(c x + d). Si
deseamos recuperar la información que aparece en la ecuación canónica y-y0 = A/(x-x0),
solo tenemos que dividir por c el numerador y denominador (para dejar
el coeficiente de x igual a 1 en el denominador) y comparar los coeficientes
obtenidos.
Por ejemplo, dada la función racional y = (4 x + 12)/(2 x -3), dividimos
numerador y denominador por 2 para obtener la expresión equivalente y = (2 x +
6)/(x -1.5). Ahora solo tenemos que comparar esa expresión con la enmarcada en
la pregunta 3, correspondiente al desarrollo de y-y0 = A/(x-x0).
Averigua de esta forma cuál es centro de esa hipérbola, cuánto
mide la distancia entre un vértice de la hipérbola y su centro, y cómo está
colocado el eje principal de la hipérbola (es decir, si es paralelo a la recta
y = x o lo es a la recta y = -x).
|