En esta actividad descubrirás cómo podemos llegar hasta las fórmulas de la longitud de la circunferencia y del área del círculo.

En el caso de la circunferencia, compararemos su longitud con la del perímetro de polígonos regulares inscritos en ella. En el caso del círculo, dividiremos esos polígonos en finos triángulos que reagruparemos formando otra figura de área conocida.

Pulsa sobre esta imagen
para ver las instrucciones de uso

Preguntas

Escena: Longitud de la circunferencia

1. Lleva el deslizador N hasta su valor mínimo (N = 8) y hazlo crecer paso a paso (N = 12, 16...). Anota en tu cuaderno, en forma de tabla, el valor de N y el correspondiente valor del semiperímetro del polígono regular. Observa la figura. ¿Qué pasa con los lados del polígono al aumentar N?

2. Si aumentásemos el valor de N mucho más que 120 (que es el máximo que permite la aplicación), ¿el valor del semiperímetro llegaría a superar el valor de la longitud de la semicircunferencia? ¿Por qué?

3. ¿Podemos concluir que el valor de la longitud de la semicircunferencia es 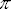veces R? ¿Cuál será entonces el valor de la longitud de una circunferencia de radio R? ¿Y la longitud de una circunferencia de diámetro D? Aplica esa fórmula para calcular la longitud de un disco de 20 cm de diámetro.

4. Si solo nos interesa un cálculo aproximado y sencillo, ¿cómo estimarías, mentalmente, el perímetro de un disco de 20 cm de diámetro?

Escena: Área del círculo

5. Lleva el deslizador N hasta el valor 60 y mueve suavemente el deslizador azul hasta arriba de todo. El círculo se ha descompuesto en 60 triángulos que se han vuelto a recomponer en un romboide. ¿Cuál es, aproximadamente, el área de ese paralelogramo?

6. Si aumentásemos el valor de N mucho más que 120, ¿en qué tipo de figura se iría convirtiendo el romboide? ¿Por qué?

7. ¿Podemos concluir que el valor del área del círculo es R veces el semiperímetro? ¿Cuál será entonces la fórmula del área de un círculo de radio R? Aplica esa fórmula para calcular el área de un disco de 20 cm de diámetro.

8. Si solo nos interesa un cálculo aproximado y sencillo, ¿cómo estimarías, mentalmente, el área de un disco de 20 cm de diámetro?