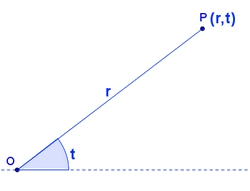
Para representar curvas como las espirales las coordenadas cartesianas que utilizamos habitualmente no resultan adecuadas. En su lugar se utilizan las coordenadas polares, en las cuales un punto cualquiera P queda determinado por su distancia r al origen O y por el ángulo t girado con respecto a la horizontal:

De este modo, la ecuación en coordenadas polares de una curva es de la forma r = f(t), una fórmula matemática que expresa la distancia al origen en función del ángulo de giro. Utilizando este tipo de coordenadas las ecuaciones de algunas espirales son:

• Espiral uniforme o de Arquímedes: r = a·t

• Espiral equiangular o logarítmica: r = a·b^t

donde r representa en ambos casos la distancia al origen y t el ángulo de giro; a  y, en su caso, b son parámetros que caracterizan a la curva.