Imagina este baile de 3 personas: la primera gira alrededor de un centro fijo, la segunda gira alrededor de la primera y la tercera alrededor de la segunda. ¿Qué recorrido hace la tercera persona al bailar? ¿Y si fuesen 4 o 5 o 6 personas, cada una girando alrededor de la anterior?

Si todas giran en el mismo sentido (horario o antihorario) y a la misma velocidad, el resultado es bastante decepcionante: todas las personas giran alrededor del centro trazando circunferencias concéntricas, cada vez un poco más amplias.

Pero si alguien cambia de sentido o velocidad la danza puede animarse bastante.

En esta actividad podrás explorar el recorrido de puntos que dan vueltas sobre puntos que dan vueltas sobre puntos que... Es decir, puntos situados en circunferencias que giran como volantes, cada volante fijado en el volante anterior. Comprobarás que los resultados serán sorprendentes en muchas ocasiones.

Preguntas

1. Mueve el punto blanco, en la circunferencia discontinua, para girar los volantes. Activa la casilla Rastro y mueve suavemente el punto blanco. También puedes seleccionarlo y pulsar las teclas + (sentido positivo ) o - (sentido negativo). ¿A qué signo, positivo o negativo, corresponden los sentidos horario y antihorario?

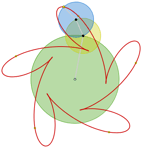2. Activa la casilla Curva y desactiva la casilla Rastro. Borra los rastros anteriores moviendo la goma de borrar. La casilla Curva muestra el trazado completo del punto situado en el último volante (el tercero, en este caso). Este trazado tiene simetría rotacional de orden 5.
   
   Activa la casilla Comprobar. Se dividirá el plano en 5 partes, una de ellas sombreada y aparecerá un punto rojo hueco en la curva roja. Puedes mover ese punto o bien la región sombreada moviendo el punto blanco. Coloca el punto rojo sobre la parte sombreada y hazlo recorrer la parte de la curva que cae dentro de esa zona para comprobar que todo el resto de la curva es una copia rotada de esa parte. Puedes desactivar momentáneamente la casilla Curva para ver mejor el repintado.

3. Eleva el número de Volantes a 4 y a 5 e intenta repetir el proceso anterior. ¿Qué observas?

4. Eleva el número de Volantes a 6 e intenta repetir el proceso anterior. ¿Qué observas?

5. Manteniendo activada la casilla Comprobar, mueve el deslizador de la velocidad v₆ del Volante 6 hasta encontrar alguna velocidad que devuelva la simetría rotacional al trazado. Para mover el deslizador con precisión puedes usar las teclas + y -. ¿Qué velocidades son válidas? Anótalas en tu cuaderno.

6. Desactiva la casilla Comprobar. En la introducción se dice que si todas las velocidades (con su sentido, es decir, con su signo) son iguales entonces el trazado es siempre circular. Compruébalo igualando las velocidades.

7. Establece el número de Volantes en 2.  Elige como v₁ = 1 y v₂ = 0. ¿Qué figura aparece? Mueve el punto blanco para observar por qué.

8. Elige como v₁ = 1 y v₂ = -1. ¿Qué figura aparece? Mueve el punto blanco para observar por qué.

9. ¿Qué sucede cuando, con esas velocidades, igualamos los radios r₁ y r₂? Mueve el punto blanco para observar por qué.

10. Mantén esos valores. Coloca el punto blanco a la derecha, de forma que los cuatro puntos se encuentren en la misma horizontal (situación inicial). El deslizador f₂ es la fase (ángulo inicial) del segundo volante respecto al primero (las demás fases siempre son también respecto al primer volante). Cuando f₂ = 0º, decimos que el volante segundo "está en fase" (es decir, tiene el mismo ángulo inicial) con el primero, y para cualquier otro valor f₂ indica el ángulo de desfase. Haz que f₂ tome los valores 90º, 180º y 270º. ¿Qué le sucede al trazado en cada caso? ¿Por qué? 

11. Prueba a darle a v₂ otros valores y observa las figuras que aparecen. En cada caso, varía también los valores de los radios r₁ y r₂ y observa las variaciones que experimenta la curva.

12. Elige v₁ = 2 y v₂ = -3. Varía los valores de los radios r₁ y r₂ y observa las variaciones que experimenta la curva.

13. Con esas mismas velocidades, elige Orden = 5 y activa la casilla Comprueba. ¿Para qué otros valores de las velocidades v₁ y v₂ el trazado vuelve a tener simetría rotacional de orden 5? Anota todos los pares de valores que encuentres en tu cuaderno. Procura ser sistemático y construye un tabla de valores: comienza por v₁ = -20, anota los valores de v₂ que mantienen la simetría rotacional, y continúa de esa forma con  v₁ = -19... hasta v₁ = 20.

14. Analiza la tabla de valores que has construido. Trata de encontrar una pauta, una ley que te permita averiguar sin comprobarlo para qué valores de v₁ y v₂ el trazado tendrá simetría rotacional de orden 5.

15. Comprueba que tu ley valga también para otros órdenes: 2, 3, 4...

16. Comprueba que tu ley valga también cuando hay más volantes: 3, 4, 5 o 6. Si no vale, intenta buscar una ley más general, que valga en todos los casos.

17. Elige cualquier trazado que tenga simetría rotacional de cualquier orden. ¿Cambia esa simetría al variar el tamaño de cualquiera de los radios de los volantes? ¿Y al variar cualquiera de las fases?

18. Elige los 6 volantes, asigna a los cuatro primeros la velocidad 1. Al quinto, asígnale velocidad 18. ¿Qué tres velocidades puede llevar el sexto volante para que el trazado tenga simetría de orden 17?

19. Elige 4 volantes. Asigna a los tres primeros volantes las velocidades 1, 2 y 3. ¿Podrás asignar alguna velocidad al cuarto volante de forma que realice un trazado que tenga simetría rotacional de orden 2? ¿Y de orden 3? ¿Por qué? ¿Puede existir alguna velocidad que provoque la aparición de algún orden de simetría rotacional en el trazado dejado por el punto del cuarto volante?

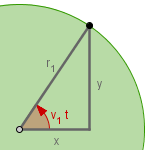20. Asigna r₄ = 1.4, r₅ = 1.5 y r₆ = 0.9. Esta combinación de valores te permitirá pasar a otro escenario en donde solo verás el primer volante. Mueve el punto blanco para hacer girar el punto negro. En la construcción, el punto gira con velocidad v₁ así que el ángulo que recorre en un tiempo t es v₁ t.
    
    Las coordenadas del punto negro son (x, y) pero observa que:
    
    x = r₁ cos(v₁ t)
    y = r₁ sen(v₁ t)
    
    Como el segundo volante gira alrededor de ese punto, habrá que sumar sus ecuaciones de giro para obtener las coordenadas (x, y) del punto que gira en el segundo volante:
    
    x = r₁ cos(v₁ t) +  r₂ cos(v₂ t + f₂)
    y = r₁ sen(v₁ t) +  r₂ sen(v₂ t + f₂)
    
    Observa que hemos añadido un ángulo inicial f₂ que es la fase del segundo volante respecto al primero. ¿Cuáles serán entonces las coordenadas (x, y) del punto que gira en el tercer volante?