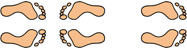
Un friso es una repetición infinita de un dibujo a lo largo de una franja comprendida entre dos rectas paralelas. Periódicamente, todo se repite exactamente igual, de tal forma que, al recorrer la franja con la vista, nos resulta imposible distinguir qué parte del friso estamos viendo en cada momento. El dibujo se traslada en una única dirección, así que para construir un friso basta usar azulejos con forma de rectángulo (o cuadrado, como caso particular de rectángulo).

Dado que la dirección elegida para construir el friso es irrelevante, consideraremos que el friso se encuentra en una franja horizontal y llamaremos eje horizontal a la recta situada a mitad de camino entre los bordes de la franja.

El motivo decorativo y la celda primitiva

Ahora bien, a su vez en cada azulejo rectangular puede aparecer el mismo dibujo, llamado motivo decorativo, repetido de distintas formas, mediante reflexiones, rotaciones o reflexiones desplazadas. Hay una infinitud de posibles formas de repetir el motivo en el azulejo, pero los matemáticos han demostrado que teniendo en cuenta las repeticiones de los motivos decorativos en él, sorprendentemente solo existen 7 maneras de disponer simetrías que distribuyan los motivos en el friso.

Solo hay 7 tipos de frisos

Pero... ¿qué sucede si deseamos cubrir la franja con azulejos de otras formas (polígonos cóncavos, por ejemplo, o triángulos o cuadriláteros cualesquiera, o figuras de animales que encajen unas con otras...), o en distintas orientaciones (girados, volteados, etc.)? Pues lo curioso es que no lograremos encontrar ni un sola posibilidad más además de esas 7. Dicho de otra forma, cualquier friso creado con otras formas y disposiciones de azulejos puede ser reproducido usando solamente azulejos rectangulares.

Cada una de esas 7 posibilidades se denomina "grupo de isometrías" del friso. Así que si vemos un friso que nos gusta mucho y queremos realizar nuestra propia versión con otros dibujos y colores pero manteniendo el mismo juego visual de simetrías, lo primero que tendremos que hacer es averiguar a qué grupo de isometrías corresponde ese friso.

Las isometrías

Las isometrías ("iso", igual; "metría", medida) son simetrías que conservan la forma y el tamaño. La homotecia (ampliación o reducción de una imagen) es una simetría en el sentido que produce una copia que conserva el aspecto de la imagen original, pero no es una isometría porque no conserva el tamaño.

Una isometría de un friso es una operación que realizamos al friso completo de forma que una vez realizada obtenemos exactamente el mismo friso original (aquí no consideramos cambios de color, solo observaremos la forma). Por ejemplo, imagina que el dibujo que aparece en la imagen anterior se repite sin fin a ambos lados. Si hacemos una copia de ese friso y la trasladamos una unidad (la distancia entre dos dibujos seguidos y congruentes), la copia y el original volverán a coincidir exactamente (como el friso es infinito no tiene extremos, así que no nos sobrará ni faltará ningún dibujo). Decimos entonces que esa traslación es una isometría de ese friso. Si reflejamos todo el friso infinito en un espejo vertical situado entre dos dibujos congruentes también volverá a coincidir con el original. Así que esa reflexión también es una isometría de ese friso.

Solo existen cuatro tipos diferentes de isometrías planas:

• Traslación. Consiste en desplazar todo el friso cierta distancia en determinada dirección. Todos los frisos tienen una única dirección en la que desplazar todo el friso sin variarlo. Las traslaciones las empleamos al colocar todos los azulejos, uno junto al otro, hasta cubrir toda la franja formando un friso infinito.

• Rotación. Consiste en girar el motivo cierto ángulo respecto a un punto (centro de rotación). Llamamos orden de rotación al divisor de 360º que nos da el ángulo. Si el orden es 1 no hay giro (360º/1 es equivalente a 0º), si el orden es 2 el giro es de 180º, si es 3 de 120º, etc. En los frisos las únicas rotaciones posibles, además de las obvias de orden 1, son las de orden 2.

• Reflexión o simetría axial. Consiste en darle la vuelta al motivo (giro espacial de 180º alrededor de una recta), o, equivalentemente, reflejarlo en un espejo (eje de reflexión). Los frisos solo pueden tener como eje de reflexión el eje horizontal (H) o ejes perpendiculares a él (que llamaremos ejes verticales V).

• Reflexión desplazada. Consiste en reflejar el motivo y después trasladar la copia medio azulejo en la dirección del eje de reflexión (piensa, por ejemplo, en las huellas que dejas al andar recto por una playa: los pies son simétricos, pero, al andar, cada pie avanza respecto al otro). En los frisos, el eje de deslizamiento solo puede ser el eje horizontal.

Combinándolas de distintas formas obtenemos cada uno de los 7 grupos.

Notación de cada grupo

Existen diversas notaciones para cada grupo de isometrías. Aquí usaremos una de las más usadas, la notación topológica de Conway. Indicamos también la notación cristalográfica por si buscas referencias en páginas web que la usen.

• El símbolo "∞" indica la limitación de cada borde entre los que se produce la traslación. Evidentemente, todos los frisos tienen dos bordes, pero en la notación solo aparecen explícitamente los dos ∞ en los grupos 1 y 5 porque en los demás grupos el segundo borde ya se crea como resultado de aplicar alguna isometría al primer borde (rotación, reflexión en el eje horizontal o reflexión con deslizamiento).

• Cada * indica una reflexión (presencia de un espejo o eje de reflexión).

• Cada número 2 indica un centro de rotación independiente de orden 2. Si el número va antes del * se trata de un centro de rotación pura (no situado en ningún espejo) y si va después se trata de un centro situado en el espejo.

• Cada x indica una reflexión desplazada.

Es importante señalar que en la notación solo aparecen los elementos independientes, es decir, aquellos que no pueden crearse  a partir del resto. Por ejemplo, en el grupo 7 hay un espejo (*) y dos centros independientes de rotación de orden 2. Al girar ese espejo mediante esas rotaciones se obtiene el otro espejo perpendicular.

Los 7 grupos de frisos

Nota: Las casillas sombreadas pueden servir como método para identificar a qué grupo corresponde un friso.

La composición y el significado de "grupo"

Una composición de isometrías es el resultado de aplicar sucesivamente dos o más isometrías. El resultado siempre será otra isometría. Todas las composiciones de isometrías de un grupo son también isometrías de ese grupo. Como existen muchas formas (en realidad, infinitas) de aplicar una isometría tras otra, podríamos pensar que acabarán apareciendo más tipos de isometrías. No es así. Lo que sucede es que los tipos de isometrías están fuertemente relacionadas entre sí por lo que muchas composiciones producen los mismos tipos. Por ejemplo, el grupo 7 tiene reflexiones en los ejes horizontal y vertical. Su composición, es decir, aplicar una reflexión y luego la otra, equivale a una rotación de 180º.

No obstante, cada grupo de frisos tiene infinitas isometrías distintas (aunque todas ellas de alguno de los cuatro tipos) debido a que podemos realizar un número infinito de traslaciones distintas.