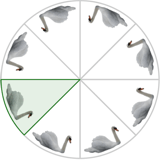
Un rosetón es una distribución regular de un dibujo alrededor de un punto fijo central. Periódicamente, cada cierto ángulo, todo se repite exactamente igual, de tal forma que, al recorrerlo con la vista, nos resulta imposible distinguir qué parte del rosetón estamos viendo en cada momento. Como el punto central se mantiene fijo, para formar un rosetón nos basta usar azulejos con forma de sector circular.

El motivo decorativo y la celda primitiva

Ahora bien, a su vez en cada azulejo con forma de "quesito" (sector circular) de cierto ángulo, puede aparecer el mismo dibujo, llamado motivo decorativo, reflejado por la bisectriz del ángulo. Si no aparece esa reflexión, la celda primitiva es todo el azulejo con forma de sector. En cambio, si aparece esa reflexión, la celda primitiva es la mitad del azulejo. Todos los rosetones son de una de estas dos clases.

Solo hay 2 clases de rosetones

Pero... ¿qué sucede si deseamos cubrir el giro de 360º con azulejos de otras formas o en distintas orientaciones (girados, volteados, etc.)? Pues lo curioso es que no lograremos encontrar ni un sola posibilidad más además de esas dos clases mencionadas. Dicho de otra forma, cualquier rosetón creado con otras formas y disposiciones de azulejos puede ser reproducido usando solamente azulejos con forma de quesito, en donde el motivo decorativo puede encontrarse reflejado o no.

Cada una de esas 2 posibilidades, junto con el orden de rotación, se denomina "grupo de isometrías" del rosetón. Así que si vemos un rosetón que nos gusta mucho y queremos realizar nuestra propia versión con otros dibujos y colores pero manteniendo el mismo juego visual de simetrías, lo primero que tendremos que hacer es averiguar a qué grupo de isometrías corresponde ese rosetón.

Observemos que cualquier valor natural de n (1, 2, 3, 4...) sirve para usar el ángulo 360º/n como ángulo de rotación. Así que para cada orden n tendremos dos grupos de isometrías (el que no tienen reflexión y el que sí). Por lo tanto, hay infinitos grupos de rosetones, pero todos ellos pertenecen a una de esas dos clases. Los grupos de la primera clase, que solo usan rotaciones, se denominan grupos cíclicos, y los de la segunda clase, que usan rotaciones y reflexiones, se llaman diedros.

Las isometrías

Las isometrías ("iso", igual; "metría", medida) son simetrías que conservan la forma y el tamaño. La homotecia (ampliación o reducción de una imagen) es una simetría en el sentido que produce una copia que conserva el aspecto de la imagen original, pero no es una isometría porque no conserva el tamaño.

Una isometría de un rosetón es una operación que realizamos al rosetón completo de forma que una vez realizada obtenemos exactamente el mismo rosetón original (aquí no consideramos cambios de color, solo observaremos la forma). Por ejemplo, si hacemos una copia del rosetón que aparece en la imagen anterior y la rotamos un ángulo dado (la distancia angular entre dos dibujos congruentes), la copia y el original volverán a coincidir exactamente. Decimos entonces que esa rotación es una isometría de ese rosetón. Si reflejamos todo el rosetón infinito en un espejo vertical situado entre dos azulejos también volverá a coincidir con el original. Así que esa reflexión también es una isometría de ese rosetón.

Solo existen cuatro tipos diferentes de isometrías planas:

• Traslación. Consiste en desplazar todo el rosetón cierta distancia en determinada dirección. Todos los rosetones carecen de traslaciones, ya que su centro se mantiene siempre fijo.

• Rotación. Consiste en girar el motivo cierto ángulo respecto a un punto (centro de rotación). Llamamos orden de rotación al divisor de 360º que nos da el ángulo. Si el orden es 1 no hay giro (360º/1 es equivalente a 0º), si el orden es 2 el giro es de 180º, si es 3 de 120º, etc. El orden de rotación del rosetón variará en función del ángulo usado para crear el azulejo con forma de sector circular.

• Reflexión o simetría axial. Consiste en darle la vuelta al motivo (giro espacial de 180º alrededor de una recta), o, equivalentemente, reflejarlo en un espejo (eje de reflexión). Los rosetones solo pueden tener como eje de reflexión rectas que pasen por su centro.

• Reflexión desplazada. Consiste en reflejar el motivo y después trasladar la copia medio azulejo  en la dirección del eje de reflexión (piensa, por ejemplo, en las huellas que dejas al andar recto por una playa: los pies son simétricos, pero, al andar, cada pie avanza respecto al otro). En los rosetones no hay reflexiones desplazadas, pues no hay traslaciones.

El primer grupo de rosetones hace uso solamente de rotaciones. El segundo, añade reflexiones.

Notación de cada grupo

Existen diversas notaciones para cada grupo de isometrías. Aquí usaremos una de las más usadas, la notación topológica de Conway. Indicamos también la notación cristalográfica por si buscas referencias en páginas web que la usen.

• Cada * indica una reflexión (presencia de un espejo o eje de reflexión).

• El número n indica el orden del centro de rotación (el punto fijo del centro del rosetón).

Es importante señalar que en la notación solo aparecen los elementos independientes, es decir, aquellos que no pueden crearse a partir del resto. Por ejemplo, en el grupo 2 hay un espejo (*) y un centro independiente de rotación. Al girar ese espejo mediante rotaciones se obtienen todos los demás espejos.

Las 2 clases de grupos de rosetones

Existen diversas notaciones para cada grupo de isometrías. Aquí usaremos una de las más usadas, la notación topológica de Conway. Indicamos también la notación cristalográfica por si buscas referencias en páginas web que la usen.

Nota: Las casillas sombreadas sirven como método para identificar a qué grupo corresponde un rosetón.

La composición y el significado de "grupo"

Una composición de isometrías es el resultado de aplicar sucesivamente dos o más isometrías. El resultado siempre será otra isometría. Todas las composiciones de isometrías de un grupo son también isometrías de ese grupo. Cada grupo de rosetones de orden n tiene un número finito de isometrías distintas (n en el caso de los cíclicos y 2n en el caso de los diedros). Veamos un ejemplo de cada clase.

Tomemos el grupo cíclico 5. En este grupo las únicas isometrías que hay son rotaciones de orden 5, es decir, solo podemos girar el azulejo un ángulo múltiplo de 360º/5 = 72º. Vemos fácilmente que aplicar 5 veces ese ángulo de giro es lo mismo que dar una vuelta completa y dejar todo como estaba. Precisamente de esta repetición cíclica deriva el nombre del grupo.

Este grupo solo tiene 5 isometrías: rotación de 72º, rotación de 144º, rotación de 216º, rotación de 288º y rotación de 360º (0º). En la siguiente imagen aparece el dibujo central de la bandera y escudo de Hong Kong. Es un perfecto rosetón del grupo 5 (y cada una de las estrellas de 5 puntas es un rosetón del grupo *5).

Tomemos ahora el grupo diedro *6. El nombre de diedro procede de las reflexiones que posee y que lo distinguen del grupo cíclico. Como ya hemos mencionado en los tipos de isometrías, una reflexión se pueden ver también como rotación espacial con ángulo diedro (es decir, ángulo entre dos planos) de 180º. La rotación plana se puede conseguir ahora como composición de reflexiones (rotaciones espaciales) sucesivas del motivo: al componer dos reflexiones conseguimos una rotación plana.

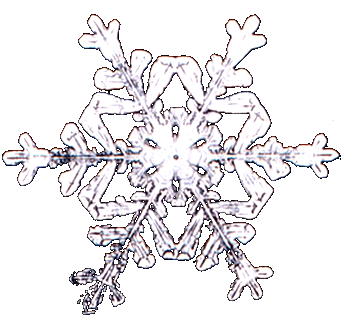
El conjunto de simetrías conseguido corresponde a las del hexágono regular: hay 12 isometrías, de las cuales 6 son  rotaciones (ángulos 60º, 120º, 180º, 240º, 300º y 0º) y las otras 6 son reflexiones sobre espejos formando ángulos de 30º. En la siguiente imagen, un cristal de nieve muestra su casi perfecta simetría *6.