|
Preguntas
-
Observa que del
rombo solamente conoces con certeza dos de sus vértices, que
son la roca y el árbol. Estos dos vértices pueden ser los
extremos de una diagonal o los extremos de uno de sus lados:
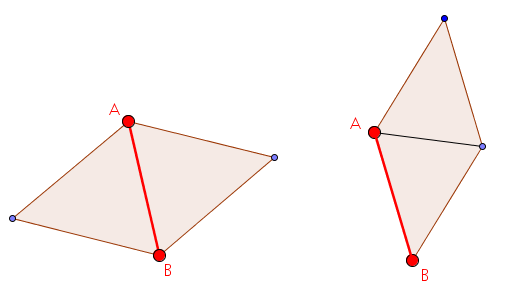
En definitiva,
¿bastan estos datos para localizar el tesoro? ¿O, por el
contrario, podrá tener más de una solución el problema?

Pulsa sobre esta imagen
si necesitas ayuda
-
Supón que se trata
del primer caso: la roca y el árbol son extremos de una
diagonal del rombo. Los otros dos vértices deben estar sobre
la otra diagonal. Traza dicha diagonal (te vendrá bien
recordar que las diagonales de un rombo son perpendiculares
y se cortan en su punto medio) utilizando las herramientas
de GeoGebra que consideres adecuadas. La intersección de
dicha diagonal con la pista te permitirá conocer la
ubicación del tercer vértice. ¿Donde estará el cuarto
vértice? Utiliza las herramientas que consideres adecuadas
para señalarlo. En ese vértice se encuentra el tesoro. Una
vez situado el cuarto vértice, dibuja el rombo.
-
Considera ahora
que la roca y el árbol son los extremos de uno de los lados
del rombo. Sabes también que otro de los vértices está en la
pista. En tal caso, la distancia desde la roca o desde el
árbol al punto que buscamos en la pista debe ser igual a la
distancia entre la roca y el árbol (recuerda que en un rombo
los cuatro lados son iguales). Por ello se nos abren varias
posibilidades.

Pulsa sobre esta imagen
si necesitas más ayuda
Abordemos una de
ellas: traza la circunferencia que tiene como centro la roca R
y pasa por el árbol A. Señala los puntos de intersección de la
circunferencia con la pista: cada uno de ellos puede ser el
tercer vértice del rombo. Localiza, en cada caso, el cuarto
vértice del rombo (ten en cuenta la simetría) y dibuja el
rombo correspondiente. Obtendrás así dos soluciones.
-
Traza ahora la
circunferencia que tiene como centro A y pasa por R. Repite
el proceso del apartado anterior con esta nueva
circunferencia.
-
Selecciona la
herramienta  Elige y Mueve. Activa la casilla Comprobar. Comprueba una a
una las soluciones del problema, activando las casillas
correspondientes.
Elige y Mueve. Activa la casilla Comprobar. Comprueba una a
una las soluciones del problema, activando las casillas
correspondientes.
-
Elabora un pequeño
informe sobre el problema. Haz un esquema en tu cuaderno,
con los datos del problema, las construcciones que has hecho
y las soluciones encontradas. Explica el procedimiento que
has seguido para hallar los puntos donde tendríamos que
cavar para estar seguros de encontrar el tesoro.
-
Si la roca y el
árbol estuvieran en otra ubicación, manteniendo fija la
pista, ¿tendríamos también 5 soluciones? Vamos a investigar.
Activa la casilla Mover roca y árbol. Mueve la roca (el
punto R) o el árbol (el punto A), observa lo que ocurre y
analiza las distintas posibilidades. ¿Puede tener una única
solución el problema? ¿Puede no tener solución?
|