Los tres vértices A, B y C de un triángulo equilátero están a la misma distancia. Los segmentos que unen esos tres puntos, es decir, los lados del triángulo, son todos de la misma longitud: AB=AC=BC.

En un triángulo isósceles ABC, en cambio, hay dos distancias distintas entre sus vértices: AB=AC y BC, por ejemplo.

Si ampliamos el número a cuatro puntos distintos, al unirlos obtenemos un total de 6 segmentos. Estos segmentos no pueden ser todos de la misma longitud (aunque en el espacio sí podrían ser, formando las aristas de un tetraedro regular, en el plano es imposible).

Ya que los 6 segmentos AB, AC, AD, BC, BD y CD no puede ser de la misma longitud, nos preguntamos si pueden ser de dos longitudes diferentes, y no más de dos, como sucedía en el triángulo isósceles. La respuesta es que sí. Por ejemplo, disponiendo los puntos como vértices de un cuadrado, como muestra la figura.

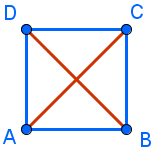
Como ves, solo hay dos longitudes diferentes:  AB=BC=CD=AD en azul y AC=BD en rojo. Dicho de otra forma, solo hay dos distancias distintas entre los cuatro puntos A, B, C y D.

Ahora bien, los cuatro puntos pueden disponerse de más formas, además de como un cuadrado, formando otras figuras que conservan esa misma propiedad: solo hay dos distancias distintas entre los cuatro puntos. En concreto, además del cuadrado, hay otras cinco disposiciones posibles.

El propósito de esta actividad es que encuentres esas cinco formas de colocar los cuatro puntos, además de la ya mostrada, de manera que solo haya dos distancias distintas entre ellos.

Preguntas

1. ¿Cómo puedes colocar tres puntos, por ejemplo A, B y C, de forma que estén a una misma distancia (a)? Construye esa figura.

2. Una vez construida la figura, ¿puedes colocar el cuarto punto (D) de forma que diste a de dos puntos y otra distancia (b) del tercero?

3. Sin mover A, B y C, ¿puedes colocar el cuarto punto (D) de forma que diste a de un punto y b de los otros dos? Hay dos formas diferentes de lograrlo.

4. Sin mover A, B y C, ¿puedes colocar el cuarto punto (D) de forma que diste b de ellos tres?

5. Si has logrado realizar los apartados 2, 3 y 4 con éxito, habrás encontrado ya cuatro de las cinco figuras que estamos buscando. Solo te falta encontrar una más. Te damos una pista: no te bases esta vez en la pregunta 1, sino más bien en la figura cuya imagen aparece en el Enunciado, intentando variar su forma un poco a la vez que se conservan solo dos distancias distintas.

6. Realiza un informe final que explique el fin de esta investigación con tus palabras y muestre las figuras encontradas, con los vértices etiquetados con letras y señalando las distancias iguales (por ejemplo: AB=BC=CD=AD y AC=BD).