|
Soluciones
-
Cualquiera que sea el valor de N la población se extingue al cabo de unos años
cuando λ<1.
-
Siendo λ<1,
cuanto más se aproxima a 1 el índice de vitalidad, más lentamente va
disminuyendo la densidad de población. Cuando λ=1 la
población también se extingue, aunque N se va acercando a 0 muy
lentamente.
-
La densidad de población
al cabo de 3 años es N=0.21672. La densidad de población tiende
a estabilizarse en torno a N=0.33333.
-
Al cabo de
muy pocos años, cualquiera que sea el valor de N (siendo 0<N<1), la densidad
de población se mantiene constante: N=0.33333.
-
En todos los casos la población
se estabiliza en torno a un valor que solamente depende de
λ.
-
Los
valores que se obtienen son los siguientes:
| Índice de vitalidad (λ) |
1.25 |
1.5 |
1.75 |
2 |
2.25 |
2.5 |
2.75 |
| Atractor (a) |
0.2 |
0.33333 |
0.42857 |
0.5 |
0.55556 |
0.6 |
0.63636 |
La relación entre el valor del atractor a y el índice de vitalidad
λ es:
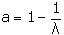
-
Conforme
vamos aumentando el valor de λ observamos que aparece un comportamiento
periódico. Por ejemplo, para λ=3 la población se estabiliza
alternadamente en valores cercanos a 0.69 y 0.64, respectivamente. Conforme
λ se va aproximando a 3.5 sigue habiendo un comportamiento periódico, pero
ahora en torno a 4 valores. Por ejemplo, si λ=3.5 la población se estabiliza
alternadamente en valores cercanos a 0.383, 0.827, 0.501 y 0.875,
respectivamente.
 |
 |
| λ=3 |
λ=3.5 |
-
Cuando λ
va tomando valores mayores que 3.5 enseguida aparece un comportamiento
caótico. Una variación de una centésima en el valor de λ provoca resultados
completamente diferentes en N, como se puede observar en las siguientes
imágenes que corresponden a λ=3.67 y λ=3.68, respectivamente. Para un mismo
valor de λ también se obtienen resultados muy dispares al variar la densidad
de población inicial:
 |
 |
| λ=3.67 N=0.5 |
λ=3.68 N=0.5 |
 |
 |
| λ=3.67 N=0.8 |
λ=3.68 N=0.8 |
-
Cuando λ>4
se obtienen resultados disparatados: aparecen valores negativos, lo cual
resulta imposible en el contexto en el que se aplica la ecuación (N
representa una densidad de población, que no puede tomar valores mayores que
1 ni menores que 0). Por tanto, cuando λ>4 el modelo no se puede aplicar. En
definitiva, el índice de vitalidad λ toma valores comprendidos entre 0 y 4.
Dentro de ese intervalo se producen situaciones deterministas, periódicas o
caóticas para la densidad de población, en función del valor que toma el
índice de vitalidad.
|