|
Soluciones
-
En la casilla e1.
-
Las cuatro posibles salidas de los caballos blancos son Ca3, Cc3, Cf3 y Ch3.
-
El peón en g2 está a 3 saltos de distancia del caballo en g1.
-
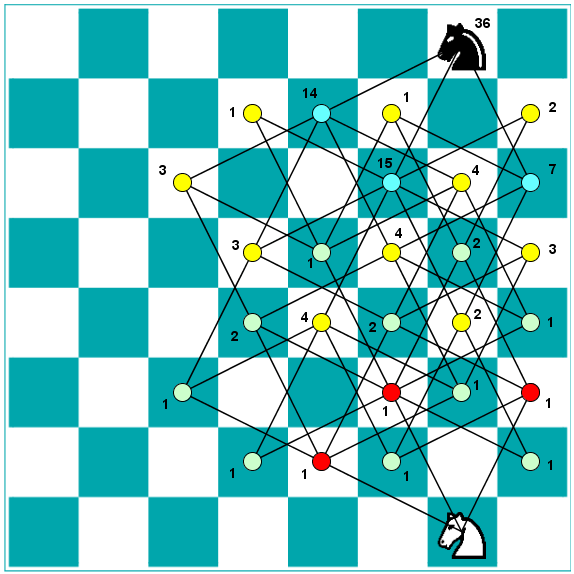
Hay 36 formas de lograrlo. En la imagen se puede ver una forma sencilla de
recuento. Empezamos señalando los puntos rojos, que están a 1 salto de
distancia. Seguimos con los puntos verdes, a 2 saltos, los amarillos situados
a 3 saltos y los azules a 4 saltos. Luego contamos, en cada punto, cuántos
caminos conducen a él, simplemente sumando el número de caminos que conducen a
los puntos que convergen en él.
-
El número total de saltos efectuados por el caballo, incluyendo el de la
captura, ha de ser forzosamente par. Esto es debido a que cada vez que el
caballo realiza un salto cambia el color de su casilla. Como la captura se
produce en una casilla negra (pues el alfil situado al inicio en f8 siempre ha
de ocupar una casilla negra), y esa casilla es del mismo color que la de
partida (g1), el número de saltos tuvo que ser par.
-
Ahora no se puede averiguar la paridad del número de saltos efectuados, pues
la dama negra puede estar situada en una casilla de cualquier color.
-
La posición final del mate del loco es la siguiente:

Es jaque mate porque el rey recibe la amenaza de la dama, no puede interponer
ninguna pieza y solo puede moverse a f2, casilla que también está amenazada.
-
El máximo número de escaques atacados a la vez corresponde a una dama colocada
en el cualquiera de los cuatro escaques del centro del tablero. Si no hay
obstáculos, la dama ataca a un total de 27 escaques.
-
Cada peón se puede mover, al inicio, de dos formas diferentes, así que hay 16
posibilidades. Cada caballo, puede saltar sobre los peones de dos formas
diferentes. Son entonces, en total, 20 posibilidades, ya que el resto de las
piezas no se pueden mover.
-
Como el primer movimiento de las blancas no interfiere en las 20 posibilidades
de primer movimiento de las negras, por cada primer movimiento blanco habrá 20
diferentes elecciones posibles de las negras. Por lo tanto, en total hay 20 x
20 = 400 posibilidades.
|