|
Soluciones
-
El área del cuadrado es de 5 cm2.
-
La longitud del segmento es
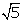 cm. Es un número irracional, por lo que no se puede expresar de manera
exacta en forma decimal.
cm. Es un número irracional, por lo que no se puede expresar de manera
exacta en forma decimal.
-
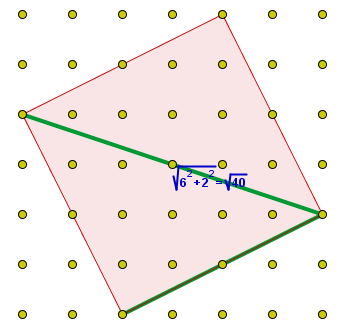
El segmento verde es la
hipotenusa de un triángulo rectángulo, que tiene un cateto horizontal de 2
cm de longitud y un cateto vertical de 1 cm de longitud. Se obtiene,
obviamente, el mismo resultado que en el ejercicio anterior.
-
El segmento tiene una longitud de
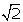 cm.
cm.
-
Se forma un segmento de longitud
doble que el anterior cuando fijado un extremo nos desplazamos 2 cm en
horizontal y otros 2 cm en vertical, hasta el otro extremo o, de otro modo, la diagonal de un
cuadrado de 2 cm de lado. Su longitud exacta es
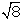 cm.
cm.
-
Teniendo en cuenta que
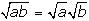 ,
en este caso tendríamos: ,
en este caso tendríamos:
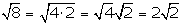
-
La longitud del segmento 3 es el
doble de la del segmento 1. La longitud de este segmento es
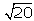 cm. La relación es
cm. La relación es
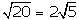
-
La medida exacta del segmento 4
es 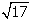 cm. No se puede construir,
uniendo puntos del geoplano, un segmento cuya longitud sea la mitad.
cm. No se puede construir,
uniendo puntos del geoplano, un segmento cuya longitud sea la mitad.
-
La relación no es cierta. En el
ejercicio 7 ya hemos visto que la relación correcta es:
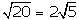 . .
-
La longitud exacta de los
segmentos es
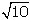 cm y
cm y
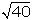 cm, respectivamente. Por tanto se confirma nuevamente que la relación por la
que se preguntaba en el ejercicio anterior no era cierta: el doble de
cm, respectivamente. Por tanto se confirma nuevamente que la relación por la
que se preguntaba en el ejercicio anterior no era cierta: el doble de
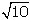 es
es 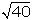 y no
y no
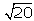 . .
-
Los segmentos tienen la misma
longitud, 5 cm.
-
Basta tomar el segmento 2 y el
segmento que se forma cuando nos desplazamos 3 cm en horizontal y otros 3 cm
en vertical, para ir de un extremo a otro según las líneas del geoplano:
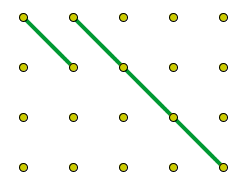
-
La medida exacta de la diagonal
es 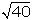 cm.
cm.
-
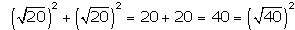 . .
-
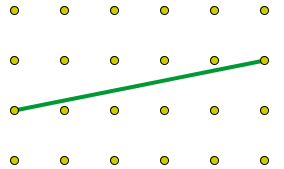
Tomando, por ejemplo, un segmento
horizontal de 5 cm y uno vertical de 1 cm, la hipotenusa medirá
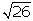 cm:
cm:
-
El lado del cuadrado mide
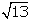 cm. Aplicando el teorema de Pitágoras:
cm. Aplicando el teorema de Pitágoras:

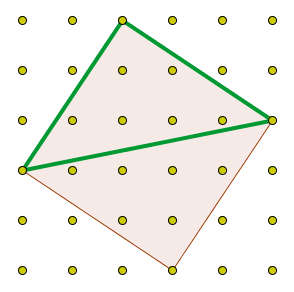
-
La diagonal es
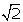 veces el lado, es decir: d=
veces el lado, es decir: d=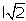
-
La longitud del lado será:
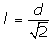
-
Todas las longitudes son raíces
de la forma
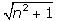 .
El segmento de longitud .
El segmento de longitud
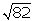 cm forma parte de esa secuencia, ya que
cm forma parte de esa secuencia, ya que
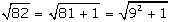 .
Sin embargo el segmento de longitud .
Sin embargo el segmento de longitud
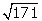 cm no forma parte de esa secuencia, puesto que 170 no es un cuadrado
perfecto.
cm no forma parte de esa secuencia, puesto que 170 no es un cuadrado
perfecto.
-
Si es a2+b2=c2,
se trata de buscar ternas pitagóricas tales que a<10 y b<15. Las soluciones
posibles son: (3, 4, 5), que es la que aparece en el ejercicio 11, (6, 8, 10),
(9, 12, 15) y (5, 12, 13).
|