Soluciones

1. La ecuación de la parábola que aparece dibujada es y=x². La ecuación de la recta es y=px+q. Los puntos de corte de la recta y la parábola cumplen ambas ecuaciones. En tales puntos se tiene x²=px+q, por tanto son las soluciones de la ecuación x² − p x − q = 0.

2. Se pueden comprobar los resultados de la tabla con la aplicación.

3. La expresión general del número metálico de orden p,q es:

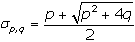
4. Solamente cuando la raíz cuadrada es exacta. En los demás casos se obtienen números irracionales, al aparecer raíces cuadradas de números que no son cuadrados perfectos.

5. Tiene que cumplirse que p² + 4q sea un cuadrado perfecto.

6. Sacando factor común 2 en σ_4,4 obtenemos el doble del número de plata σ_2,1:

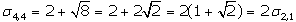
7. El número de bronce es igual al de níquel más uno: σ_3,1=σ_1,3+1

8. Desarrollando el cubo de Φ obtenemos:
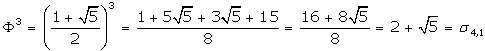