|
Soluciones
-
Si partimos de AB=1:
-
HF = 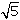 /2 /2
-
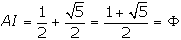
-
AP = AI = Φ
-
La razón entre la diagonal y el
lado es Φ.
-
Las diagonales forman un
polígono estrellado de 5 puntas, también llamado pentalfa o pentagrama
místico. Las intersecciones de las diagonales determinan un pentágono
regular.
-
Los lados son AB=1, AD=BD=Φ.
Los ángulos miden A=72º, B=72º y D=36º.
-
La razón de semejanza es
Φ, ya que:
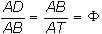
-
Los triángulos ABT y AST son
semejantes y la razón de semejanza también es Φ.
-
Tienen los ángulos
correspondientes iguales (A=A, B=S, C=B) y sus lados correspondientes
proporcionales, siendo Φ la razón de semejanza:
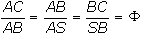
-
Se construye el rectángulo
áureo que tiene por lados la diagonal del pentágono regular y su lado, AC y
AB. Con el lado AB común, se construye a continuación el rectángulo áureo de
lados AB y AS. Por último, con el lado AS común, se construye el rectángulo
áureo de lados AS y ST.
|