|
Soluciones
-
Se percibe
con bastante claridad que aparece más a menudo el semáforo en rojo que en
verde, es decir, sucede más a menudo que la aguja toque alguna de las líneas
de la trama que no las toque.
-
Como era fácil
suponer, las posibilidades de que al caer la aguja toque alguna de las
líneas de la trama disminuyen a medida que acortamos su longitud: cuanto más
corta es la aguja más probable es que no toque una de las líneas de la trama.
-
Solamente se
trata de observar lo que ocurre al activar la animación.
-
Tomando los
datos de varias simulaciones y hallando el valor medio, el resultado
obtenido será aproximadamente 0,64.
-
Al aumentar el
valor de n, las variaciones de p con respecto al valor medio obtenido en el
apartado anterior serán cada vez menores. La probabilidad que cabe asignar
al suceso sería 0,64, que es el valor al que se acerca p. Por ello cabe
esperar que el número de agujas que toquen alguna de las rayas de la trama
al hacer 1000 lanzamientos sea de unas 640.
-
Repitiendo
varias veces la simulación, anotando en cada caso el valor de p y hallando
el valor medio, el resultado que se obtiene es aproximadamente 0,32.
Observamos que cuando la longitud de la aguja es de 0,5 unidades la
probabilidad es aproximadamente la mitad que cuando la longitud era de 1
unidad.
-
Cuando la
longitud es de 0,25, la probabilidad es aproximadamente la mitad que en el
caso anterior o,
también, la cuarta parte de la que se obtenía cuando la longitud era 1. Con
longitudes de 0,2, 0,4, 0,6 y 0,8 los valores de p resultan, aproximadamente,
0,13, 0,25, 0,38 y 0.51, respectivamente. Concluimos que la probabilidad
estudiada es
directamente proporcional a la longitud de la aguja.
-
Al calcular el
valor medio el valor que se obtiene es, aproximadamente, 3,14.
-
La probabilidad,
del suceso "lanzar una aguja sobre el rayado y que toque una de las líneas
paralelas", cuando la longitud es 0,5, es:
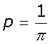
-
La probabilidad
p, en función de la longitud l de la aguja viene dada por la expresión:
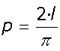
NOTA: La fórmula
anterior es aplicable cuando la distancia entre las rayas rectas paralelas
es de 1 unidad y la longitud de la aguja es menor o igual que dicha
distancia. Para una distancia d y para valores de l menores o iguales que d
la probabilidad vendría dada por la expresión:
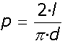
|