Soluciones

1. El cilindro recorre 2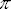 en cada vuelta, por tanto su radio mide 1 (unidad lineal).

2. Al rodar el cilindro, el arco de hélice repite una y otra vez la gráfica de la función f(x) = x - 2 en el intervalo [0, 2).

3. La periodicidad es de 2.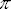

4. La gráfica dibujada por el cilindro al rodar no es continua porque los valores en los extremos del intervalo no son iguales: f(0) = -2 mientras que f(2) = 2 - 2.

5. La función es f(x) = a x + b. Al variar "a" se modifica la pendiente de la recta y, además, de manera inversamente proporcional, el radio del cilindro. Al variar b se modifica la ordenada en el origen de esa recta. La altura del cilindro se ajusta automáticamente a esa posición, pero variar b no altera su radio porque no cambia la periodicidad.

6. Cuando a = 2, el cilindro recorre en cada vuelta, por tanto su radio mide 1/2 (unidades lineales). La periodicidad es ahora de .

7. En cada vuelta el cilindro recorre 2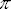, por tanto su radio mide 1 (unidad lineal).

8. La periodicidad es de 2.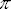

9. La función es f(x) = sin(a x + b), es decir, el seno de una función afín. Al variar "a" se modifica la pendiente de la recta y, además, de manera inversamente proporcional, el radio del cilindro. Al variar b se modifica la ordenada en el origen de esa recta (ángulo inicial o fase de la función seno). El borde elíptico del cilindro se ajusta automáticamente a esa fase, pero variar b no altera su radio porque no cambia la periodicidad.

10. Cuando a = 2, el cilindro recorre en cada vuelta, por tanto su radio mide 1/2 (unidades lineales). La periodicidad es ahora de .

11. Con el cilindro detenido, al mover b, el punto que está dibujando el cilindro se mueve verticalmente debido a que las variaciones de b afectan a la posición de la elipse (ordenada del punto) pero la posición del cilindro no varía (abscisa constante). Al punto le sucede lo mismo que a una boya al paso de una ola.

12. El intervalo es [0, 2), por lo que la periodicidad es 2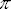. La gráfica resultante es continua porque los valores en los extremos del intervalo son iguales: f(0) = = f(2).