Soluciones

1. Las dos bobinas no giran siempre a la misma velocidad: cuanta menos cinta enrollada tienen más rápido giran. En consecuencia los radios varían también a distinto ritmo.

2. La longitud total de la cinta es: 50·4.5=225 cm. Al cabo de 10 s en la bobina izquierda la cinta enrollada mide 10·4.5=45 cm. En la bobina derecha quedarán: 225-45=180 cm.

3. La longitud de la cinta enrollada en la bobina de la derecha va disminuyendo a un ritmo constante de 4.5 cm/s. El esbozo de la gráfica debería mostrar un segmento rectilíneo que une los puntos (0,225) y (50,0), representando en el eje vertical la longitud de la cinta, en centímetros, y en el eje horizontal el tiempo, en segundos.

4. La aplicación permite comprobar los resultados.

5. La expresión algebraica sería: L=225-4.5 t, donde L es la longitud de la cinta enrollada en la bobina de la derecha, en centímetros, y t el tiempo que lleva en funcionamiento la casete, en segundos.

6. La aplicación permite comprobar todos los resultados que se piden.

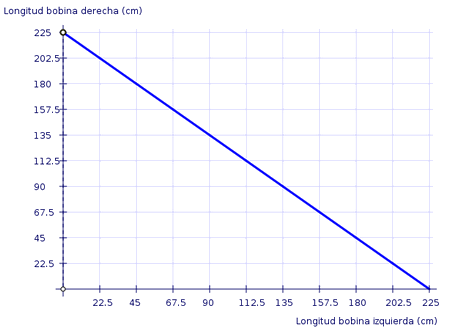
7. Si la longitud de la cinta de la bobina izquierda es de 55 cm, la cinta en la bobina derecha mide 225-55=170 cm. Si l_i es la longitud de la cinta enrollada en la bobina izquierda y l_d la de la cinta enrollada en la bobina derecha: l_d=225-l_i. La representación gráfica sería:

8. La distancia entre las bobinas es de 5 mm cuando empieza a girar la casete, va disminuyendo hasta algo menos de 2 mm, que se alcanzan cuando va a mitad de recorrido, y vuelve a aumentar hasta llegar al final a la misma distancia de 5 mm que había al principio.

9. La aplicación permite comprobar los resultados. La gráfica de la función es un arco de parábola, comprendido entre los puntos (0,5) y (50,5) y vértice en (25,1.92).

10. La expresión algebraica que nos da la distancia d entre las bobinas, en milímetros, en función del tiempo t, en segundos. redondeando a una cifra significativa en cada uno de los coeficientes, es la siguiente: d=0.005·t²-0.2·t+5.

11. Los contadores solamente muestran el mismo resultado cuando la cinta empieza a girar y cuando completa su recorrido y cambia el sentido de giro. El contador que muestra el número de vueltas de la bobina de la izquierda aumenta rápidamente al principio pero el ritmo al que aumenta se va reduciendo conforme pasa el tiempo. Cuanto mayor es el radio de la bobina, más cinta es necesaria para envolverla y, como la cinta avanza a velocidad constante, más lentamente aumenta el contador. En el contador que muestra el número de vueltas de la bobina de la derecha sucede lo contrario: el radio va disminuyendo, por lo que el contador cada vez aumentará más rápido. Finalmente las dos bobinas habrán dado el mismo número de vueltas, por lo que cuando paramos la cinta al final del recorrido los mostradores indican el mismo resultado.

12. La aplicación permite comprobar el resultado.

13. La aplicación muestra la gráfica que se pide.

14. La aplicación permite comprobar los resultados.

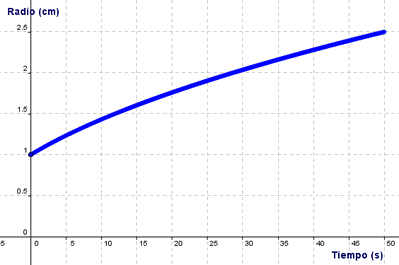
15. La gráfica que muestra la variación del radio de la bobina de la izquierda con el tiempo es:

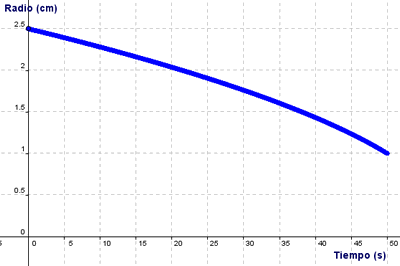
16. La gráfica que muestra la variación del radio de la bobina de la derecha con el tiempo es: