|
Soluciones
-
Llegaría al punto de no retorno
justamente a las 2 horas de haber salido, por tanto el PNR estaría a 500 km
del aeropuerto de salida.
-
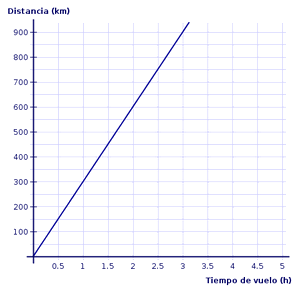
La velocidad real
a la que vuela, es decir, la velocidad con respecto al suelo, sería de 300
km/h. Gráficamente estaría representado por una recta de pendiente 300 que
parte del origen de coordenadas. La expresión algebraica sería d = 300 t,
siendo d la distancia al
aeropuerto y t el tiempo transcurrido desde el despegue.
-
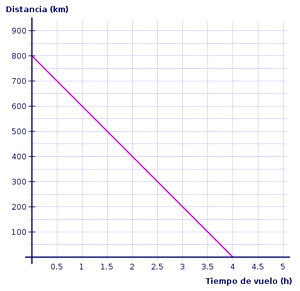
En el viaje de vuelta el avión
volará a 200 km/h Gráficamente estaría representado por una recta de
pendiente -200 que pasa por el punto (4,0). La
expresión algebraica que nos da la distancia d al aeropuerto en función del
tiempo t en el viaje de vuelta sería: d = -200 (t-4) = -200 t +
800.
-
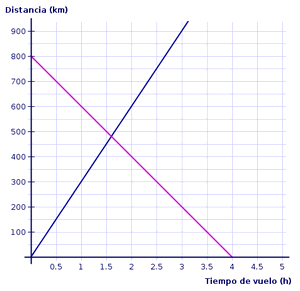
Si representamos las dos gráficas
anteriores en los mismos ejes, el PNR estaría representado por el punto de
intersección de las dos rectas. De ese modo podemos leer que la distancia es
de algo menos de 500 m y el tiempo es algo superior a 1.6 horas. Resolviendo
el sistema de ecuaciones formado por las dos expresiones algebraicas podemos
calcular las coordenadas del PNR con más precisión: está situado a 480 m de
la salida y debe iniciar el regreso al cabo de 1.6 horas.
-
El PNR cambia cuando se modifica la
velocidad del viento: describe una parábola de eje vertical, que corta al
eje de abscisas en los puntos (0,0) y (4,0). El vértice de la parábola, que
es el punto (2,500), coincide con el PNR cuando el viento está en calma.
-
Un valor negativo significa que
el viento sopla en sentido contrario al avance del avión en el viaje de ida.
-
La gráfica siempre es una
parábola de eje vertical, que corta al eje de abscisas en los puntos (0,0) y
(4,0). Al modificar la velocidad del avión cambia la curvatura de la
parábola, determinada por la posición del vértice. En todos los casos el
vértice de la parábola coincide con PNR cuando el viento está en calma, es
decir, por la distancia que recorre el avión, sin viento, durante 2 horas.
-
En todos los casos la gráfica es
una parábola de eje vertical, que corta al eje de abscisas en los puntos
(0,0) y (ta,0), siendo ta el tiempo de autonomía de vuelo, cuyo vértice tiene
por coordenadas la mitad del tiempo de autonomía de vuelo y la distancia que
recorre el avión, sin viento, durante ese tiempo, respectivamente.
-
La tabla quedaría como sigue:
|
Tiempo del viaje de ida (h) |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
|
Distancia del PNR al aeropuerto (km) |
0 |
218.8 |
375 |
468.8 |
500 |
468.8 |
375 |
218.8 |
0 |
-
Activando
la casilla "Tabla de valores" se comprueba el resultado.
-
La expresión algebraica es: d
= -125t2 + 500t.
-
El PNR cuando el viento
está en calma se corresponde con el vértice de la parábola. Si la velocidad
del avión es va y el tiempo de autonomía ta, las coordenadas del
PNR, o lo que es lo mismo, las coordenadas del vértice de la parábola, serían
(ta/2, va·ta/2).
-
Se trata de hallar la ecuación de
una parábola que pasa por los puntos (0,0), (0,ta) y (ta/2,
va·ta/2). El
resultado que se obtiene, una vez simplificado, es: d = -2vat2/ta
+ 2vat, siendo d la distancia del PNR al aeropuerto de partida,
en km, t el tiempo empleado en alcanzar el PNR, en horas, va la
velocidad del avión, en km/h, y ta su autonomía de vuelo, en horas. La
velocidad del viento no interviene en la expresión algebraica.
-
El resultado que se obtiene, una
vez simplificada la expresión, es:
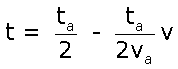
-
El resultado que se obtiene, una
vez simplificada la expresión, es:
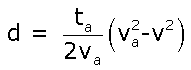
|