Soluciones

  1. La distancia del vértice al origen es 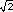. Por tanto, la distancia del foco al origen será 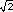veces (que es la excentricidad) esa distancia 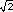, es decir, 2. Es decir, el foco está situado en el vértice opuesto al origen de un cuadrado cuya diagonal mide 2. Por lo tanto, el lado de ese cuadrado debe ser f = 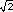 y las coordenadas (f, f) del foco F son (, ).

  2. Tenemos que X = f - SF, por tanto X = - SF. Tenemos que Y = PS + f, luego Y = PS + .  Además, ST = SR = X porque el triángulo RST tiene por ángulos 90º, 45º y 45º (la recta directriz tiene pendiente -1, así que forma un ángulo de -45º con la horizontal). Luego RST es isósceles, además de rectángulo.

  3. El triángulo DTP es un triángulo isósceles rectángulo porque sus ángulos son 90º, 45º y 45º (la recta directriz tiene pendiente -1, así que forma un ángulo de -45º con la vertical).

  4. Como PT2 = DT2 + PD2, entonces PT2 = PD2 + PD2 = 2 PD2, por lo que PT = PD.

  5. Como (PS + ST)2 = PS2 + SF2, entonces PS2 + 2 PS ST + ST2 = PS2 + SF2, luego ST2 + 2 PS ST = SF2.

  6. Como X2 + 2 (Y - ) X = ( - X)2, entonces X2 + 2 Y X - 2 X = 2 -2 X + X2, de donde Y = 1/X.

  7. Efectivamente, al mover el punto A se comprueba en distintas posiciones que sus coordenadas cumplen la relación Y = 1/X (cualquier posible desviación es debida al redondeo).

  8. Porque el área del cuadrado rojo es 1 (ya que su lado mide 1) y el área del rectángulo amarillo es X Y. Ahora bien, el rectángulo amarillo se forma con las coordenadas (X, Y) de un punto de la hipérbola cuya ecuación es precisamente X Y = 1.