|
Soluciones
-
La igualdad Y = -1/X
puede interpretarse como que el área del rectángulo de dimensiones X y "-Y" es
1.
-
Al aplicar una homotecia centrada
en el origen con factor k, el punto (1, 0) se traslada a una distancia k veces
1, es decir, a (k, 0), y el punto (0, 1) se traslada a (0, k). Por tanto, el
vértice en V (1, 1), se trasladará a V' (k, k). (Un razonamiento equivalente
se obtiene aplicando el teorema de Tales.) Dicho de otra forma, el homólogo de
(x, y) será siempre (k x, k y).
-
Como y/k = 1/(x/k), entonces y/k
x/k = 1, es decir, x y = k2, de donde
y = k2/x. (Por supuesto, operando con las fracciones se
alcanza el mismo resultado.)
-
El significado geométrico que tiene el valor absoluto de la constante A,
es decir, k2, es el del área del cuadrado determinado por el origen
y el vértice de la hipérbola o de cualquier rectángulo determinado por el
origen y un punto cualquiera de la hipérbola. El signo de A determina la
colocación de la hipérbola (1º y 3º cuadrantes si es positivo, 2º y 4º si es
negativo). Si el valor absoluto de A es k2, las coordenadas
de los vértices serán (k, signo(A) k) y (-k, -signo(A) k).
-
Basta ver la ecuación y = A/x
para poder afirmar, sin necesidad de ver la gráfica, que representa a una
función impar porque si sustituimos "x" por "-x" la ordenada cambia de signo,
que es justo el efecto que produce una reflexión a través del origen de
coordenadas.
-
Las coordenadas de
los vértices de la hipérbola y = 4/x son (2, 2) y (-2, -2), pues como A es 4,
k ha de valer 2. Como las distancias de los focos al origen guardan la
proporción
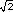 , sus
coordenadas serán (2 , sus
coordenadas serán (2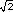 , 2 , 2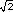 )
y (-2 )
y (-2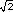 , -2 , -2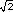 ). ).
-
El área del rectángulo que tiene
como par de vértices opuestos el origen de coordenadas y un punto de la
hipérbola y = -7/x es el valor absoluto de -7, es decir, 7 unidades cuadradas.
|