|
Soluciones
-
Si las coordenadas de V son (k,
k) entonces el numerador de la fracción en la ecuación es k2 si V
está en el primer cuadrante y es -k2 si V está en el segundo
cuadrante.
-
Si las coordenadas de V son (k,
k) entonces el numerador de la fracción en la ecuación es (k - x0)2
si V está a la derecha de C y es -(k - x0)2 si V está a
la izquierda de C.
-
Como y = A/(x-x0) + y0,
entonces y = A/(x-x0) + y0(x-x0)/(x-x0)
= (A + y0(x-x0))/(x-x0), de donde:
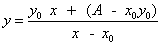
-
Como y = (2 x + 6)/(x -1.5),
entonces x0 = 1.5, y0 = 2, así que el centro de esa
hipérbola es (1.5, 2). A su vez, 6 = A -x0 y0, así que
obtenemos el valor A = 9.
Es decir, la hipérbola corresponde a una traslación de la hipérbola y = 9/x,
que a su vez corresponde a una homotecia de factor k = 3 (pues 32 = 9)
de la hipérbola básica Y = 1/X. Por tanto el vértice dista 3 unidades del
centro y, como el signo del numerador (1) es positivo, su eje principal es
paralelo a la recta y = x.
|