|
Soluciones
Escena: Ángulo central y ángulo inscrito
-
Cuando el ángulo
central azul toma los valores 60º, 80º y 100º, el ángulo amarillo mide,
respectivamente, 30º, 40º y 50º, es decir, para el mismo arco BC, el ángulo
central azul siempre mide el doble que el
correspondiente ángulo inscrito amarillo.
Escena: Posición 1 (O está en un borde del ángulo inscrito)
-
El triángulo AOB
es isósceles porque AO y BO son radios de la misma circunferencia.
-
La suma de esos
dos ángulos amarillos es el ángulo suplementario del ángulo naranja porque la
suma de los tres ángulos del triángulo AOB tiene que valer 180º.
-
El ángulo
suplementario del ángulo naranja es el azul, ya que ambos forman el ángulo
llano AOC.
Escena: Posición 2 (O está en el interior del ángulo inscrito)
-
Se puede deducir
que el ángulo central azul es el doble que el ángulo inscrito amarillo, pues
hacer el doble de una suma es lo mismo que sumar el doble de cada sumando.
Escena: Posición 3 (O está en el exterior del ángulo inscrito)
-
Se puede deducir
que el ángulo central azul es el doble que el ángulo inscrito amarillo, pues
hacer el doble de una diferencia es lo mismo que restarle al doble del
minuendo el doble del sustraendo.
Conclusiones
-
De los tres casos
(posiciones 1, 2 y 3) se puede deducir que siempre va a suceder que el ángulo
central medirá el doble que el ángulo inscrito que abarque el mismo arco BC,
puesto que O tiene que estar forzosamente en alguna de esas tres posiciones (o
está dentro, o fuera, o en el borde del ángulo inscrito).
-
Todos los ángulos
inscritos que abarcan el mismo arco BC miden lo mismo porque todos valen la
mitad que el ángulo central que abarca BC.
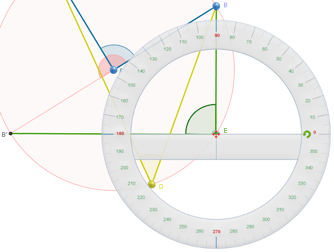
Escena: Caso importante
-
El ángulo
inscrito amarillo mide 90º y no varía al mover A. Se trata de un caso
particular de lo planteado en la pregunta 7, ya que el ángulo central azul y
el ángulo inscrito amarillo abarcan el mismo arco BC.
-
Dada una
circunferencia, cualquier punto de ella formará con los extremos de
cualquier diámetro un ángulo de 90 grados.
-
Cualquier
triángulo inscrito en una circunferencia que tenga su diámetro como uno de
los lados será un triángulo rectángulo.
|
