Soluciones

1. Son opuestos por el vértice los ángulos A y C y también B y D. Los ángulos opuestos por el vértice son iguales. La relación no cambia al cambiar la posición de las rectas.

2. Podemos encontrar cuatro parejas de ángulos adyacentes: A y B, B y C, C y D y D y A. Los ángulos adyacentes forman un ángulo llano, por tanto suman 180º. Son, por tanto, ángulos suplementarios. La relación no cambia cuando se mueven las rectas.

3. 180 - 37 = 143. Por tanto, los ángulos serían A = C = 37º y B = D = 143º.

4. Hay cuatro pares de ángulos correspondientes: A y E, B y F, C y G, D y H. Dos ángulos correspondientes son iguales. Aunque se muevan las rectas, la relación entre los ángulos correspondientes se mantiene: los pares de ángulos correspondientes siempre son iguales.

5. Son ángulos alternos internos el B y H y el C y E. Dos ángulos alternos internos son iguales. La relación no cambia aunque se muevan las rectas.

6. Son alternos externos el A y el G, así como el D y el F. Los ángulos alternos externos son iguales. La relación no cambia aunque se muevan las rectas.

7. El ángulo A también mide 42º porque A y C son opuestos por el vértice. El ángulo G mide 42º porque C y G son correspondientes. El E también mide 42º porque A y E son alternos internos. El ángulo B mide 138º, porque C y B son adyacentes. El D mide 138º porque es opuesto por el vértice a B. El F mide 138º porque es correspondiente con el B. El H mide 138º porque es alterno interno a B. Hay otras formas de establecer relaciones entre estos ángulos, pero se llegaría al mismo resultado.

8. En este caso: H = F = B = D = 64º. E = G = A = C = 116º. Los razonamientos son análogos a los del ejercicio anterior.

9. Se pueden colocar las rectas para que los ocho ángulos sean iguales: la recta transversal estará perpendicular a las dos paralelas. De ese modo los ángulos serían todos de 90º.

10. No se puede conseguir, porque los ángulos E y C son alternos internos y, por tanto, tienen que ser iguales.

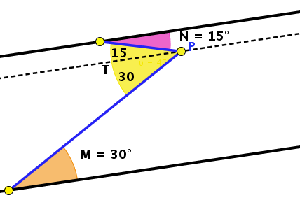
11. El ángulo T mide 45º. Como se ve en el dibujo, al trazar por el punto P la recta paralela a las otras dos paralelas, el ángulo T queda dividido en dos partes. Una de las partes mide 30º, porque es el ángulo alterno interno a M, y la otra 15º, porque es el alterno interno a N. Por tanto el T es la suma de ambos: 30 + 15 = 45.

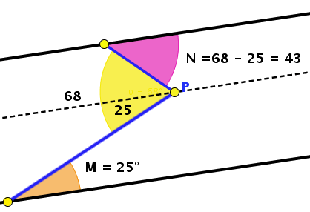
12. El ángulo N mide 43º (68-25=43). El razonamiento es similar al del ejercicio anterior. El ángulo de 68 se puede descomponer en dos, uno de ellos igual a M y el otro a N (en ambos casos, alternos internos).