|
Soluciones
-
Cuando R = 4, la
longitud de la semicircunferencia es 12.5664 (aproximadamente). A medida que
el número N de lados del polígono aumenta, los lados se aproximan más y más
a la circunferencia hasta confundirse con ella.
| N |
Perímetro |
| 8 |
12.2459 |
| 12 |
12.4233 |
| 16 |
12.4858 |
| ... |
... |
| 60 |
12.5606 |
| ... |
... |
| 120 |
12.5649 |
-
Si aumentásemos
el valor de N mucho más que 120 (que es el máximo que permite la
aplicación), el valor del semiperímetro nunca llegaría a superar el valor de
la longitud de la semicircunferencia, porque por muchos lados que tenga el
polígono inscrito siempre estará en el interior. Cada lado del polígono
inscrito unirá dos puntos de la circunferencia con un segmento, que al ser
recto siempre será más corto que el arco (curvo) con el que los une la
circunferencia.
-
Podemos concluir
que el valor de la longitud de la semicircunferencia es
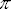 veces R, pues podemos imaginar una circunferencia como un polígono de
un número "infinito" de lados. Entonces, el valor de la longitud de una
circunferencia de radio R es 2 veces R, pues podemos imaginar una circunferencia como un polígono de
un número "infinito" de lados. Entonces, el valor de la longitud de una
circunferencia de radio R es 2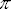 R, y la longitud de
una circunferencia de diámetro D será R, y la longitud de
una circunferencia de diámetro D será
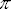 D. En el caso de que
el diámetro sea de 20 cm, la longitud será 20 D. En el caso de que
el diámetro sea de 20 cm, la longitud será 20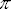 = 62.83...
= 62.83...
-
Como
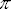 es ligeramente mayor que 3, el perímetro de un disco de 20 cm de diámetro
será poco más de tres veces 20 cm, es decir, poco más de 60 cm.
es ligeramente mayor que 3, el perímetro de un disco de 20 cm de diámetro
será poco más de tres veces 20 cm, es decir, poco más de 60 cm.
Escena: Área del círculo
-
El área de ese
romboide es aproximadamente
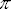 R por R, ya que R es casi la altura del
paralelogramo. R por R, ya que R es casi la altura del
paralelogramo.
-
El romboide se
iría convirtiendo en un rectángulo, porque al ser la base de cada triángulo
cada vez más pequeña, los lados iguales de esos triángulos isósceles cada
vez forman un ángulo mayor con la base, es decir, cada vez están "más
rectos".
-
Podemos concluir
que el valor del área del círculo es R veces el semiperímetro
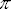 R,
es decir, la fórmula del área de un círculo de radio R es R,
es decir, la fórmula del área de un círculo de radio R es
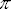 R2. En el
caso de que el diámetro sea de 20 cm, el área será 100 R2. En el
caso de que el diámetro sea de 20 cm, el área será 100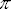 = 314.15...
= 314.15...
-
Como
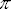 es ligeramente mayor que 3, el perímetro de un disco de 20 cm de diámetro
(10 cm de radio) será poco más de tres veces el cuadrado de 10 cm, es decir,
poco más de 300 cm2.
es ligeramente mayor que 3, el perímetro de un disco de 20 cm de diámetro
(10 cm de radio) será poco más de tres veces el cuadrado de 10 cm, es decir,
poco más de 300 cm2.
|