Soluciones

Soluciones

Se trata únicamente de familiarizarse con los controles de la aplicación.
El segmento representa la distancia entre dos vueltas consecutivas de la espiral. Excepto en la primera vuelta, la distancia entre dos vueltas consecutivas de la espiral se mantiene constante. Es la característica fundamental de una espiral uniforme o arquimediana.
Al aumentar el valor de a también aumenta la distancia entre las vueltas de la espiral. Si a=0.5 la distancia es 3.14; si a=1, la distancia es 6.28. La distancia es igual a la longitud de una circunferencia de radio a.
Se sigue manteniendo lo anterior cuando se cambia el sentido de la espiral. Para un determinado valor de a, la distancia es la misma cualquiera que sea el sentido de giro de la espiral arquimediana.
Al desplazar el punto blanco hacia el centro de la espiral vamos enrollando el hilo alrededor de la circunferencia central.
Si se cambia el sentido de giro de la espiral ocurre lo mismo que se ha indicado en el ejercicio anterior.
Anudamos el lápiz en un extremo de la cuerda. A continuación, manteniendola tirante, vamos enrollando la cuerda alrededor del bote mientras dibujamos con el lápiz sobre el papel. De ese modo el lápiz dibujará una involuta del círculo, que se completará cuando hayamos enrollado toda la cuerda alrededor del bote.
Al mover el punto sobre la curva el ángulo que forma la tangente con el segmento que une el punto con el centro de la espiral (radio vector) se mantiene constante. La espiral logarítmica se llama también equiangular porque el ángulo comprendido entre el radio vector de un punto y la tangente es constante.
Al cambiar el valor de b también cambia el ángulo comprendido entre un radio vector y la tangente. Cuando b=1 el ángulo es de 90º. La espiral se convierte en una circunferencia. A medida que aumentamos el valor de b la espiral es más abierta.
El valor del ángulo formado por la tangente y un radio vector no cambia cuando modificamos el valor de a.
En la siguiente imagen se muestra el ajuste del nautilus con una espiral logarítmica, en sentido horario, con parámetros a=0.27 y b=1.19. La longitud y giro de la curva se corresponden, respectivamente, con n=20.6 y a=72^o.

Conseguimos el ajuste que se muestra a continuación con una espiral arquimediana, en sentido antihorario, con parámetro a=0.08. La longitud y giro de la curva se corresponden, respectivamente, con n=32.5 y a=155^o. Así pues, el cantero no cumplió finalmente el deseo de Jacob Bernouilli, que era esculpir una espiral logarítmica.

Podemos lograr el ajuste que se ve en la imagen para la escultura con una espiral arquimediana, en sentido horario, con parámetros a=0.27 y b=1.19. La longitud y giro de la curva se corresponden, respectivamente, con n=38.1 y a=284^o.

Conseguimos un ajuste razonable para el fósil con una espiral logarítmica, en sentido antihorario, con parámetros a=0.12 y b=1.12. Para la longitud tomamos n=25.8 y no es necesario girar la curva.

En la siguiente imagen se muestra el ajuste de la voluta con una espiral logarítmica, en sentido antihorario, con parámetros a=0.62 y b=1.12. La longitud y giro de la curva se corresponden, respectivamente, con n=15.8 y a=58^o.

En el caso de la escultura tenemos dos espirales simétricas, una a cada lado. El ajuste de la imagen se consigue con dos espirales arquimedianas, con parámetro a=0.08 y sentidos antihorario y horario, respectivamente. La longitud y giro de la espiral izquierda son, respectivamente, con n=17.2 y a=72^o. Para la espiral derecha son: n=17.2 y a=219^o.

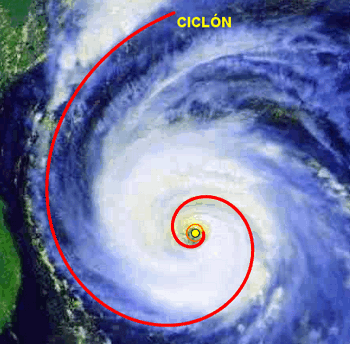
Ajustamos una de las ramas del ciclón con una espiral logarítmica, en sentido horario, con parámetros a=0.21 y b=1.35. La longitud y giro de la curva se corresponden, respectivamente, con n=10.9 y a=0^o. Con los mismos parámetros (es decir, la misma forma espiral), si vamos variando el ángulo de giro de la curva obtenemos las otras ramas del ciclón.

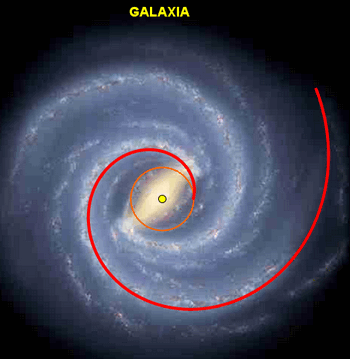
Conseguimos un ajuste razonable para una de las ramas de la galaxia con una espiral logarítmica, en sentido antihorario, con parámetros a=0.84 y b=1.3. La longitud y giro de la curva se corresponden, respectivamente, con n=6.9 y a=0^o. Con los mismos parámetros (es decir, la misma forma espiral), si vamos variando el ángulo de giro de la curva obtenemos las otras ramas de la galaxia.