|
Soluciones
-
En principio los datos que
se proporcionan son insuficientes para determinar una única
solución. Como puede verse en la Ayuda que se proporciona, a partir
de dos vértices de un rombo podrían hacerse hasta 5 interpretaciones
diferentes que darían lugar, por tanto, a 5 soluciones diferentes.
-
Las dos diagonales del
rombo se cortan perpendicularmente en sus puntos medios. Por tanto
los otros dos vértices del rombo estarán situados sobre la mediatriz
de la diagonal que forman la roca y el árbol.
-
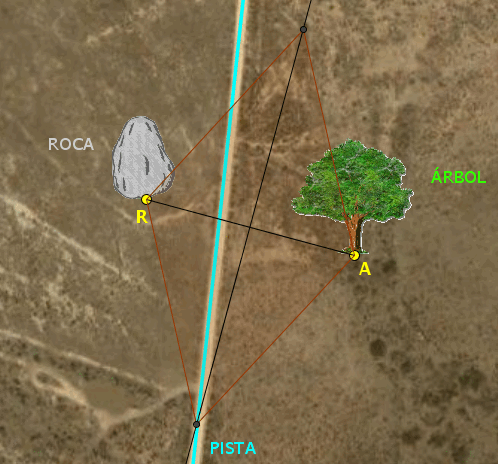
La construcción que se
obtiene se muestra a continuación. El cuarto vértice, es decir, el
punto donde estaría situado el tesoro, es el punto simétrico del
punto de corte de la mediatriz y la pista con respecto a la diagonal
que une la roca y el árbol. Puede obtenerse de manera sencilla con
la herramienta
Refleja Objeto en Recta. También podrían obtenerlo trazando la
circunferencia de centro en el centro del rombo y que pasa por el
punto de corte de la mediatriz y la pista. El otro punto de corte de
esta circunferencia con la mediatriz sería el cuarto vértice.
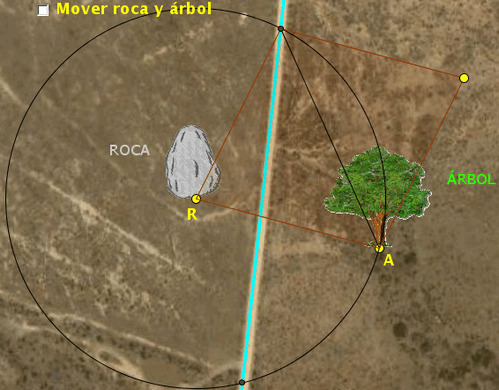
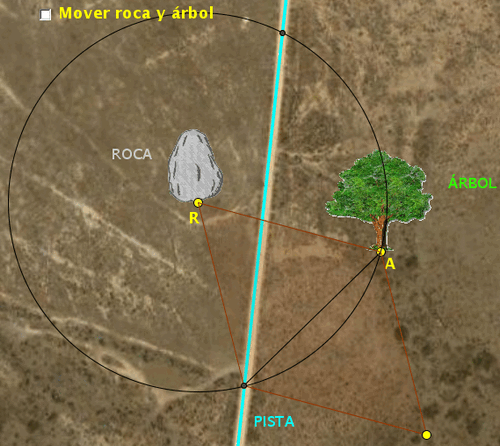
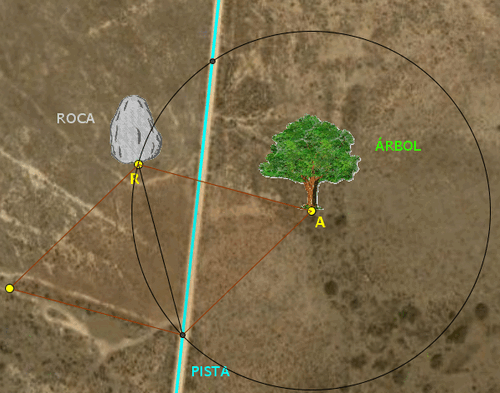
Tal como se explica en la
Ayuda, si AR es uno de los lados del rombo, lo que buscamos es un
punto de la pista que diste de R la distancia AR o que diste de A la
distancia AR. Si llamamos P a ese punto, lo que estamos haciendo es
que el lado del rombo sea BP o AP, respectivamente. En cada uno de
los casos vamos a obtener dos soluciones, puesto que hay dos puntos
de la pista que cumplen esa condición (las circunferencias, de
centros A o R, respectivamente, y radio AR cortan en dos puntos a la
pista), por lo que tendremos así otras cuatro soluciones. Se explica
el procedimiento para hallar la primera de las dos soluciones que se
obtienen a partir de la circunferencia de centro en R y radio AR.
Puede ser una de las siguientes:
-
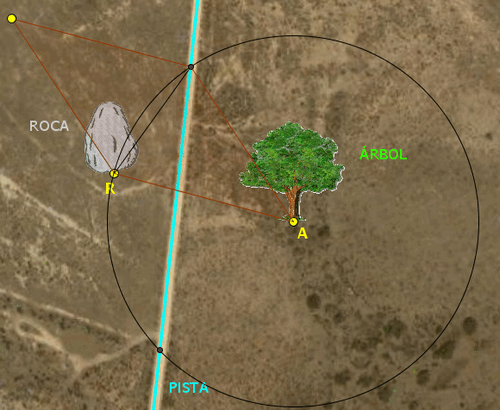
Siguiendo el mismo
proceso, pero ahora con la circunferencia de centro en A y radio AR
se obtienen otras dos soluciones, que son las siguientes:
-
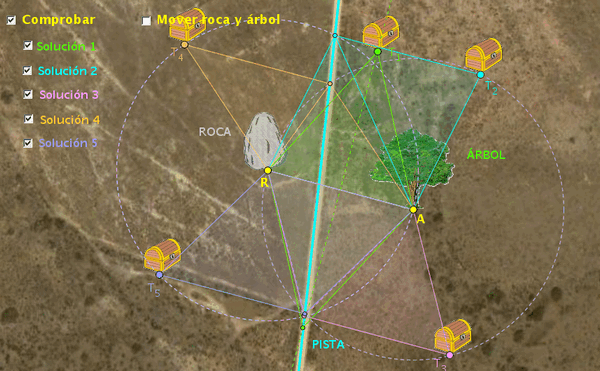
Al comprobar se pueden
observar de una manera más clara las cinco soluciones que se han
obtenido:
-
Se trata de recoger en el
cuaderno las soluciones anteriores, explicando el procedimiento
seguido para obtenerlas. Es importante que la conclusión sea que
para tener la seguridad de encontrar el tesoro sería necesario cavar
en los cinco lugares encontrados.
-
Al mover los puntos A y R
podrán ir observando que no siempre se obtienen las 5 soluciones. Lo
realmente interesante de esta actividad es que, a través de la
manipulación de los puntos, puedan razonar por qué sucede eso. Las
explicaciones razonables que cabe esperar es que dependerá de que la
mediatriz del segmento AR o las circunferencias de centros A o R,
respectivamente, y radio AR corten a la pista. La mediatriz no
cortará a la pista cuando AR es perpendicular a la misma. Las
circunferencias no cortarán a la pista cuando la distancia de A a la
pista o de R a la pista sea mayor que AR. Obtenemos cinco soluciones
cuando AR no es perpendicular a la pista y las distancias desde A y
desde R a la pista son menores que AR. A continuación se muestran
algunos ejemplos:
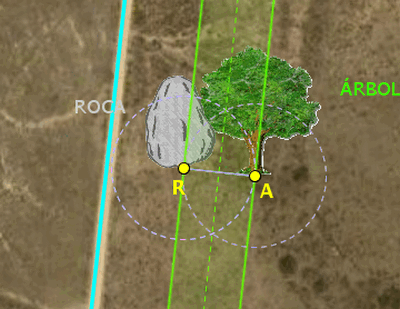
Sin soluciones
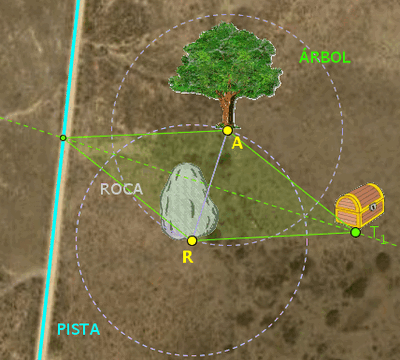
Una solución
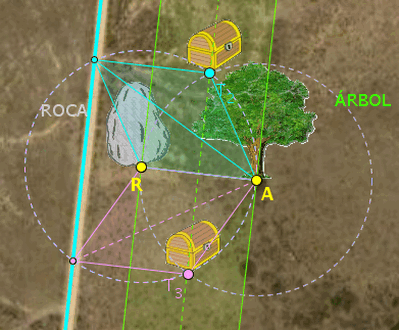
Dos soluciones
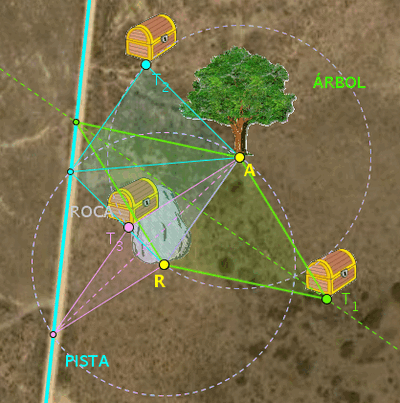
Tres soluciones
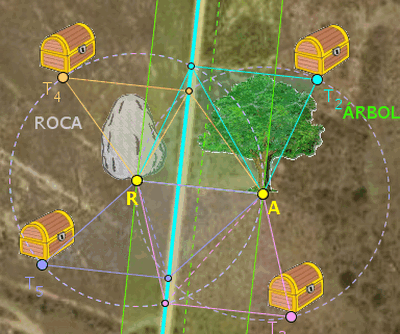
Cuatro soluciones
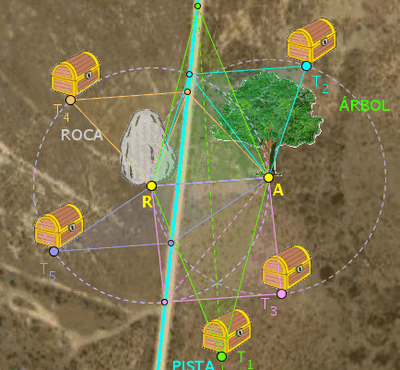
Cinco soluciones
|