Soluciones

1. Siguiendo literalmente las instrucciones se obtiene algo similar a lo representado a continuación:

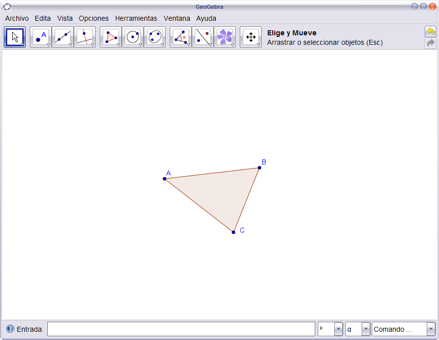
2. Con la herramienta Polígono Regular se construyen los triángulos equiláteros sobre los lados, de modo que queden orientados hacia el exterior del triángulo, obteniendo así la siguiente construcción:

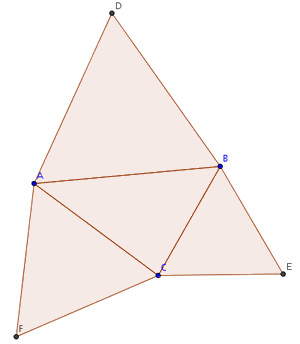
3. Con dos mediatrices en cada triángulo equilátero se puede determinar su centro. A continuación se ocultan las mediatrices dejando solamente a la vista los centros de los triángulos:

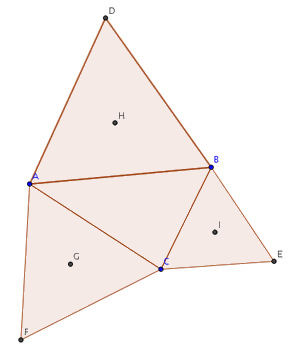
4. Se crea el triángulo cuyos vértices son los centros de los triángulos equiláteros anteriores y se cambian sus propiedades (color y grosor) de modo que quede un poco más resaltado:

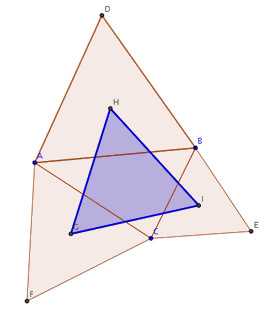
5. Al medir los lados del triángulo se puede comprobar que tienen la misma longitud. Por tanto es un triángulo equilátero.

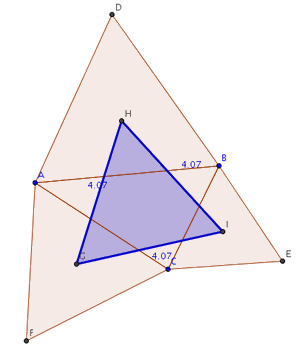
6. Al mover los puntos del triángulo inicial no cambia el tipo de triángulo que hemos obtenido al unir los centros, sigue siendo un triángulo equilátero.

7. El enunciado que cabe esperar será similar al siguiente: Si sobre los lados de un triángulo cualquiera construimos, hacia el exterior, triángulos equiláteros, el triángulo que se forma al unir los centros de dichos triángulos es un triángulo equilátero.

8. El teorema también se verifica si los triángulos equiláteros se construyen hacia el interior del triángulo:
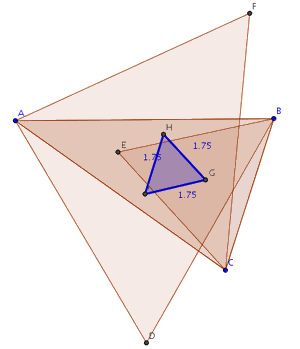