|
Soluciones
-
La aplicación no deja elegir (3;2) porque se obtendría el mismo resultado que
con (3;1), ya que saltar dos en un sentido equivale a saltar 1 (tres menos
dos) en el otro sentido.
-
Con (4;2) se obtienen dos diámetros en vez de un polígono porque 2 es la mitad
de 4. Al saltar exactamente la mitad, nos encontramos en el vértice
exactamente opuesto, así que al unirlos obtenemos diámetros.
-
La aplicación no deja elegir (5;3) porque se obtendría el mismo resultado que
con (5;2), ya que saltar tres en un sentido equivale a saltar 2 (cinco menos
tres) en el otro sentido.
-
No existe el polígono estrellado de 6 puntas. La estrella de 6 puntas se forma
por superposición de dos triángulos equiláteros.
-
La tabla queda cubierta de la siguiente forma:
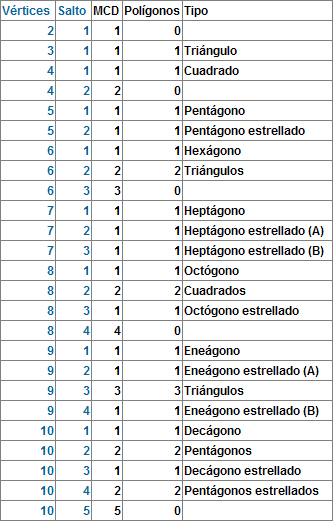
-
Se forman diámetros cuando el número de vértices es par y elegimos como salto
exactamente la mitad de ese número, es decir, en los casos de la forma (2s;s).
-
Se obtiene un único polígono regular siempre que saltamos 1, es decir, en
todos los casos de la forma (v;1), siempre que el número de vértices (v) sea
como mínimo 3.
-
Se obtiene un polígono estrellado siempre que no estemos en uno de los casos
anteriores y los dos números (vértices y salto) sean primos entre sí, es
decir, no tengan divisores propios comunes.
-
Se forman varios polígonos superpuestos en todos los demás casos, es decir,
cuando el máximo común divisor de los dos números (vértices y salto) es mayor
que 1 y no son uno el doble del otro.
-
Cuando se forman polígonos superpuestos, se forman tantos como indique el
Máximo Común Divisor. Cada uno de esos polígonos tendrá tantos vértices como
indique el cociente entre el número de vértices original y el MCD. Dicho de
otra forma, en esos casos (v;s) equivale a MCD polígonos del tipo (v/MCD;
s/MCD).
|