-
Porque si en cada vértice concurren varios polígonos
iguales, el ángulo interior de cada uno de esos polígonos tiene que ser un
divisor de 360º. En la siguiente tabla se observa que solo cumplen esta
condición los triángulos equiláteros, los cuadrados y los hexágonos
regulares:
| Número de lados del polígono regular |
Ángulo interior |
Divisor de 360º |
| 3 |
60º |
Sí |
| 4 |
90º |
Sí |
| 5 |
108º |
No |
| 6 |
120º |
Sí |
| > 6 |
> 120º y < 180º |
No |
-
El código del mosaico formado por triángulos
equiláteros es 3.3.3.3.3.3, el formado por cuadrados es 4.4.4.4 y el
formado por hexágonos regulares es 6.6.6.
-
Se pueden construir dos mosaicos
semirregulares combinando triángulos equiláteros y
cuadrados: el mosaico 3.3.3.4.4, con cuadrados contiguos, y el mosaico
3.3.4.3.4, con cuadrados alternos.
-
No se pueden construir mosaicos semirregulares utilizando únicamente cuadrados y hexágonos.
Pero podemos hacerlo con ayuda de algún otro polígono. Hay dos formas: con
ayuda de un triángulo podemos construir el mosaico 3.4.6.4 y con ayuda de
un dodecágono podemos construir el mosaico 4.6.12.
-
Podemos combinar triángulos y hexágonos únicamente de dos
formas distintas: 3.3.3.3.6 y 3.6.3.6.
-
Solo quedan dos mosaicos semirregulares más: 4.8.8 y 3.12.12.
-
Los ocho mosaicos semirregulares son
3.3.3.4.4, 3.3.4.3.4, 3.4.6.4, 4.6.12, 3.3.3.3.6, 3.6.3.6,
4.8.8 y 3.12.12.
|
Mosaicos semirregulares |
|
3.3.3.4.4
 |
3.3.4.3.4
 |
3.4.6.4
 |
4.6.12
 |
|
3.3.3.3.6
 |
3.6.3.6
 |
4.8.8
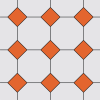 |
3.12.12
 |
-
El criterio que nos permite determinar cuándo un polígono
regular se puede combinar con otros para formar un mosaico semirregular es
si su ángulo exterior (lo que deja para que otros polígonos lo cubran) se
puede poner como suma de ángulos interiores de otros polígonos. En la
siguiente tabla vemos el resultado (no consideramos los polígonos de 7 y
11 lados por no ser divisores de 360):
| Número de lados del polígono regular |
Ángulo interior |
Suma de interiores |
| 3 |
60º |
4x60º + 1x120º = 360º
3x60º + 2x90º = 360º
2x60º + 2x120º = 360º
1x60º + 2x150º = 360º
1x60º + 2x90º + 1x120º= 360º |
| 4 |
90º |
1x60º + 2x90º + 1x120º= 360º
1x90º + 2x135º = 360º
1x90º + 1x120º + 1x150º= 360º |
| 5 |
108º |
|
| 6 |
120º |
4x60º + 1x120º = 360º
2x60º + 2x120º = 360º
1x60º + 2x90º + 1x120º= 360º
1x60º + 2x90º + 1x120º= 360º
1x90º + 1x120º + 1x150º= 360º |
| 8 |
135º |
1x90º + 2x135º = 360º |
| 9 |
140º |
|
| 10 |
144º |
|
| 12 |
150º |
1x60º + 2x150º = 360º
1x90º + 1x120º + 1x150º= 360º |