Halla la distancia mínima del punto 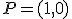a la parábola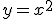

Sea 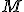el punto medio de un segmento dado 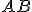. Encuentra el lugar geométrico de los puntos 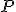del plano tales que 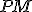es media proporcional de 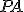y .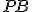

En el cuadrado de vértices A, B, C y D, de lado a, se trazan los arcos BD y AC con centro en C y en D respectivamente, y radio a. Los dos arcos se cortan en M. Hallar el radio del círculo inscrito en el triángulo curvilíneo DMC.

Se considera el triángulo ABC en el que A = 70º, B = 60º, y el triángulo A'B'C' formado por los pies de las alturas del ABC. Hallar los ángulos A', B', C'.

Dados dos puntos A y B de la Tierra, supuesta esférica, tales que AB = 60º, hallar la relación entre las alturas x e y, a que deben elevarse dos observadores en las verticales de A y de B para que puedan verse y su valor concreto cuando sea x = y.

Hallar los polígonos regulares cuyos ángulos miden un número entero de grados.

Calcula la superficie de una plaza cuadrada sabiendo que si colocamos un trozo de carne en un punto de la misma y hay tres perros situados en vértices consecutivos, el primero debe recorrer 60 metros, el segundo 48 y el tercero 36.