Si no lo has hecho ya, lee primero la información general sobre los grupos de isometrías de los mosaicos periódicos, pulsando sobre la siguiente imagen:

Grupos de isometrías de mosaicos

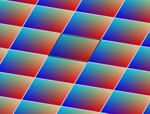
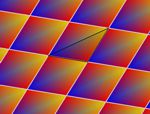
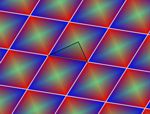
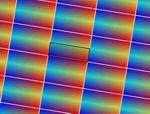
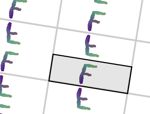
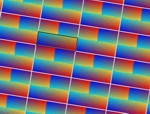
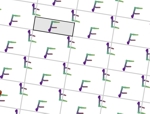
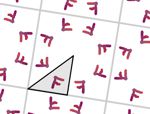
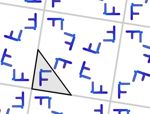
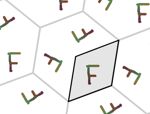
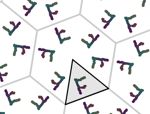
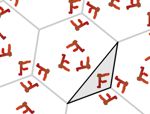
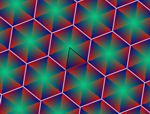
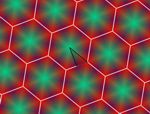
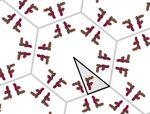
En esta actividad podrás crear tu propio diseño de mosaico. Para ello primero deberás elegir el grupo de isometrías, es decir, los tipos de simetrías que deseas que aparezcan. Más abajo tienes un ejemplo de cada grupo.

Advierte que, además de esta actividad, dispones de otras actividades específicas para cada uno de los grupos, del 1 al 17, que te permitirán explorarlos con mayor profundidad.

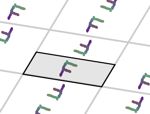
Una vez elegido el grupo, puedes mover los vértices del azulejo que se repite por traslación y dibujar el motivo decorativo en la región sombreada (celda primitiva). El lápiz se coge por su extremo superior. Es recomendable realizar movimientos suaves, especialmente cerca de los bordes de la celda primitiva. Para mover el punto sin que deje rastro de color, desactiva temporalmente la casilla Rastro.

Nota: si tienes problemas para mover el lápiz con continuidad, y ves que se mueve "a saltos", prueba con esta otra versión que consume menos memoria: Creador v2.

Los 17 grupos de mosaicos periódicos

Aquí puedes ver un par de imágenes de ejemplo de cada uno de los grupos. Todas las imágenes están realizadas usando el color automático asignado por la aplicación (opción recomendada), pero también puedes asignar otros colores manualmente. Puedes agrandar las imágenes pulsando sobre ellas.