|
En nuestra vida cotidiana utilizamos constantemente los números. ¿Te imaginas un mundo sin números? Piensa por un momento cómo viviríamos si no existieran los números. Los utilizamos para contar, para expresar el resultado de una medida, para realizar cálculos... Incluso utilizamos números para codificar información de lo más diversa: textos, imágenes, sonidos, videos...
A lo largo de la historia, las civilizaciones utilizaron diferentes sistemas de numeración. De algunos de ellos, como el romano o el sexagesimal de la antigua Babilonia, todavía quedan algunos vestigios en nuestra sociedad actual, todavía se escribe en algunos casos el año MMX o la hora 18:56, por ejemplo.
Nuestro sistema de numeración actual es un sistema posicional y decimal. Decimos que es posicional porque el valor de una cifra depende del lugar que ocupa en el número: el primer 7 del número 757 no vale lo mismo que el segundo 7. El valor del segundo 7 es siete unidades, pero el valor del primer 7 es de 700 unidades.
Decimos que es decimal porque diez unidades de un determinado orden equivalen a una unidad del orden superior. Así, diez unidades son una decena; diez decenas son una centena, diez centenas forman un millar, etc. Por ello, un número es igual a la suma de los productos de sus cifras por sus valores respectivos. Por ejemplo, el número 75.269 se puede descomponer de la siguiente manera:
75.269 = 70.000 + 5.000 + 200 + 60 + 9 = = 7x10.000 + 5x1.000 + 2x100 + 6x10 + 9
Para representar números menores que la unidad utilizamos las mismas relaciones de equivalencia entre órdenes de unidades, pero ahora en orden decreciente. Surgen así las décimas, centésimas, milésimas, diezmilésimas, etc. También podemos descomponer un número decimal de manera análoga a como lo hemos hecho antes. Por ejemplo, el número 72,483 se puede descomponer de la siguiente manera:
72,483 = 70 + 2 + 0,4 + 0,08 + 0,003 = = 7x10 + 2 + 4x0,1 + 8x0,01 + 3x0,001
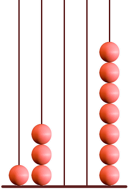
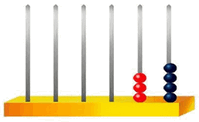
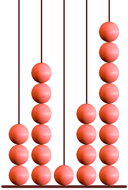
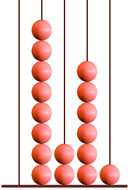
El ábaco es un instrumento que permite comprender muy bien la relación entre las unidades de distinto orden y también efectuar operaciones aritméticas sencillas. En algunos países, a pesar de la irrupción de las calculadoras electrónicas, todavía es bastante frecuente ver a algunas personas haciendo cálculos con el ábaco. En su versión más simple, un ábaco es un artilugio formado por una base horizontal con varias varillas verticales, en las que se insertan "cuentas" (anillas o bolitas perforadas). Cada varilla corresponde a un orden de unidades: cuando en una varilla se reúnen 10 cuentas se quitan y se sustituyen por una anilla o bola en la varilla que queda a su izquierda.
Representación del número 34 en un ábaco
Existen otros sistemas posicionales distintos del decimal. En informática, por ejemplo, se emplean los sistemas binario, octal y hexadecimal. En el sistema binario dos unidades de un orden equivalen a una del orden superior, por eso es un sistema que utiliza solamente unos y ceros. En el sistema octal la equivalencia entre unidades es de 8. En el sistema hexadecimal, 16 unidades de un orden equivalen a una del orden superior, por eso se emplean 16 dígitos: a los diez del sistema decimal se añaden las letras A, B, C, D, E, y F.
En la primera escena de la aplicación vamos a representar diferentes números en el ábaco. Para cambiar el número representado debes utilizar el deslizador horizontal que aparece debajo del número:
Para tener más sensibilidad en la selección de un número es aconsejable que utilices las teclas flecha. Haz clic sobre el botón del deslizador y usa la tecla flecha hacia la derecha o hacia la izquierda (si mantienes pulsada la tecla Ctrl al pulsar una tecla flecha, irá diez veces más rápido).
Escena 2 La segunda escena de la aplicación nos permitirá comprender las equivalencias entre distintos sistemas de numeración. Dispones de dos deslizadores: uno de ellos te permite seleccionar el número en la base decimal y el otro la otra base a la que lo queremos transformar. El ábaco representa en número en la base seleccionada.
Escena 3 En la tercera escena, usaremos el ábaco para representar números decimales.
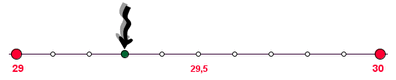
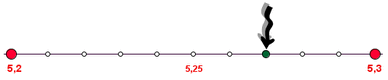
Escena 4 Por último, la cuarta escena nos permitirá representar números decimales sobre la recta numérica. Usa el deslizador horizontal para seleccionar el número. A la derecha debes representar el número de tres formas distintas: el número exacto, el número redondeado a las centésimas y el número redondeado a las décimas. En los tres casos debes hacer los mismo: colocar la flecha sobre el valor que consideres oportuno. A continuación puedes comprobar tus resultados activando las casillas de control. |
|
Preguntas Sistema decimal de numeración (escena 1)
a)
Otros sistemas de numeración (escena 2)
Números decimales (escena 3)
Representación de decimales (escena 4)
|

 b)
b)
 c)
c)